Các câu hỏi tương tự
Cho hàm số f(x) có đạo hàm f(x) liên tục trên R và thỏa mãn
f
(
x
)
∈
[
-
1
;
1
]
với
∀
x
∈
(
0
;
2
)
Biết f(0) f(2) 1 Đặt
I
∫
0
2
f
(
x
)
d
x
phát bi...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên R và thỏa mãn f ' ( x ) ∈ [ - 1 ; 1 ] với ∀ x ∈ ( 0 ; 2 ) Biết f(0) = f(2) = 1 Đặt I = ∫ 0 2 f ( x ) d x phát biểu dưới đây là ĐÚNG ?
![]()
![]()
![]()
![]()
Hàm số yf(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng? (*): y 3 là tiệm cận ngang (*): Tập xác định
D
ℝ
/
2
(*): Max y 3 (*): Min y -1 (*):
x
C
Đ
2
Đọc tiếp
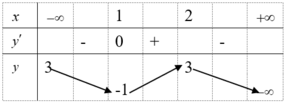
Hàm số y=f(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng?
(*): y = 3 là tiệm cận ngang
(*): Tập xác định D = ℝ / 2
(*): Max y = 3 (*): Min y = -1
(*): x C Đ = 2
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có bảng biến thiên như bên dưới. Có bao nhiêu phát biểu sau đây là đúng?
*
x
C
Đ
1
*
x
C
T
2
*
m
a
x
y...
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như bên dưới.
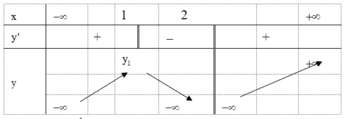
Có bao nhiêu phát biểu sau đây là đúng?
* x C Đ = 1 * x C T = 2 * m a x y = y 1
A. 2
B. 3
C. 4
D. 5
Cho đồ thị
(
C
)
:
y
x
+
1
x
2
-
4
. Có bao nhiêu phát biểu dưới đây là đúng? (*) x2 và xx-2 là TCĐ. (*) y0 là TCN. (*)
y
↓
/
ℝ
(*) Hàm số không có GTLN (max y). (*) Hàm số không có GTNN (min y). A. 2 B. 3 C. 4 D....
Đọc tiếp
Cho đồ thị ( C ) : y = x + 1 x 2 - 4 . Có bao nhiêu phát biểu dưới đây là đúng?
(*) x=2 và xx=-2 là TCĐ.
(*) y=0 là TCN.
(*) y ↓ / ℝ
(*) Hàm số không có GTLN (max y).
(*) Hàm số không có GTNN (min y).
A. 2
B. 3
C. 4
D. 5
Biết luôn có hai số a, b để
F
(
x
)
a
x
+
b
x
+
4
(
4
a
-
b
≠
0
)
là nguyên hàm của hàm số f(x) và thỏa mãn
2
f
2
(
x
)
...
Đọc tiếp
Biết luôn có hai số a, b để F ( x ) = a x + b x + 4 ( 4 a - b ≠ 0 ) là nguyên hàm của hàm số f(x) và thỏa mãn 2 f 2 ( x ) = ( F ( x ) - 1 ) f ' ( x ) . Khẳng định nào dưới đây đúng và đầy đủ nhất?
![]()
![]()
![]()
![]()
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số yf(x) với bảng biến thiên dưới đây. Trong số các kết luận sau, có bao nhiêu kết luận đúng? (*)
x
C
T
0
(*)
x
C
Đ
2
(*)
y
m
a
x...
Đọc tiếp
Cho hàm số y=f(x) với bảng biến thiên dưới đây.
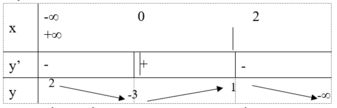
Trong số các kết luận sau, có bao nhiêu kết luận đúng?
(*) x C T = 0
(*) x C Đ = 2
(*) y m a x = 2
(*) TCN:y=2
(*) TCĐ là x = 0 và x = 2
A. 2
B. 3
C. 4
D. 5
Hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
-
3
)
với mọi x. Phát biểu nào sau đây đúng? A. Hàm số có 1 điểm cực đại B. Hàm số không có cực trị C. Hàm số có 2 điểm cực trị D. Hàm số có đúng 1 điểm cực trị
Đọc tiếp
Hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x - 3 ) với mọi x. Phát biểu nào sau đây đúng?
A. Hàm số có 1 điểm cực đại
B. Hàm số không có cực trị
C. Hàm số có 2 điểm cực trị
D. Hàm số có đúng 1 điểm cực trị
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
v
ớ
i
a
,
b
,
c
,
d
∈
ℝ
,
a...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8



