Các câu hỏi tương tự
Cho 2 hàm số
f
(
x
)
x
2
và
g
(
x
)
x
1
2
. Biết rằng α 0, f(α) g(α). Khẳng định nào sau đây là đúng? A. 0 α 1/2 B. 0 α 1 C. 1/2 α 2 D. α 1
Đọc tiếp
Cho 2 hàm số f ( x ) = x 2 và g ( x ) = x 1 2 . Biết rằng α > 0, f(α) < g(α). Khẳng định nào sau đây là đúng?
A. 0 < α < 1/2
B. 0 < α < 1
C. 1/2 < α < 2
D. α > 1
Cho hàm số f(x) xác định trên
ℝ
-
2
;
1
thỏa mãn
f
(
x
)
1
x
2
+
x
-
2
;
f
(
0
)
...
Đọc tiếp
Cho hàm số f(x) xác định trên ℝ \ - 2 ; 1 thỏa mãn f ' ( x ) = 1 x 2 + x - 2 ; f ( 0 ) = 1 3 và f(3)-f(-3) = 0 Tính giá trị của biểu thức T = f(-4)+f(-1)-f(4)
![]()
Tìm tất cả các giá trị thực của tham số
α
và
β
sao cho hàm số sau luôn giảm trên R?
y
f
(
x
)
-
x
3
3
+
1
2
sin
α
+
cos
α
x...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số α và β sao cho hàm số sau luôn giảm trên R? y = f ( x ) = - x 3 3 + 1 2 sin α + cos α x 2 - 3 2 x sin α cos α - β - 2
A. π 12 + k π ≤ α ≤ π 4 + k π , k ∈ ℤ , β ≥ 2 .
B. π 12 + k π ≤ α ≤ 5 π 12 + k π , k ∈ ℤ , β ≥ 2 .
C. α ≤ π 4 + k π , k ∈ ℤ , β ≥ 2 .
D. α ≥ 5 π 12 + k π , k ∈ ℤ , β ≥ 2 .
Cho hàm số f(x) xác định trên
R
{
-
1
;
1
}
thỏa mãn f(x)
2
x
x
2
-
1
và
f
(
-
2
)
3
,
f
(
-
1...
Đọc tiếp
Cho hàm số f(x) xác định trên R \ { - 1 ; 1 } thỏa mãn f'(x)= 2 x x 2 - 1 và f ( - 2 ) = 3 , f ( - 1 2 ) = 2 Giá trị của biểu thức f(-2)+f( 1 2 ) bằng
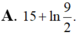
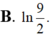
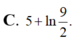
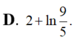
Cho hàm số f(x) xác định trên
ℝ
1
2
thỏa mãn
f
(
x
)
2
2
x
-
1
;
f
(
0
)
v
à
f
(
1
)
2...
Đọc tiếp
Cho hàm số f(x) xác định trên ℝ \ 1 2 thỏa mãn f ' ( x ) = 2 2 x - 1 ; f ( 0 ) v à f ( 1 ) = 2 Giá trị của biểu thức f ( - 1 ) + f ( 3 ) bằng:
A. 4+ln15
B. 2+ln15
C. 3+ln15
D. ln15
Cho hàm số f(x) xác định trên
R
{
1
2
}
thỏa mãn
f
(
x
)
2
2
x
-
1
f (0) 1 và f(1) 2. Giá trị của biểu thức f(-1)+f(3) bằng A.
4
+
l
n...
Đọc tiếp
Cho hàm số f(x) xác định trên R \ { 1 2 } thỏa mãn f ' ( x ) = 2 2 x - 1 f (0) = 1 và f(1) = 2. Giá trị của biểu thức f(-1)+f(3) bằng
A. 4 + l n 15
B. 2 + ln 15
C. 3+ ln 15
D. ln 15
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
(
0
a
≠
1
)
qua điểm I(2; 1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ( 0 < a ≠ 1 ) qua điểm I(2; 1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Biết
F
(
x
)
a
ln
|
x
-
1
|
+
b
ln
|
x
-
2
|
(
a
,
b
∈
Z
)
là một nguyên hàm của hàm số
f
(
x
)
x
+...
Đọc tiếp
Biết F ( x ) = a ln | x - 1 | + b ln | x - 2 | ( a , b ∈ Z ) là một nguyên hàm của hàm số f ( x ) = x + 1 ( x - 1 ) ( x - 2 ) . Giá trị của biểu thức b-a bằng
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]