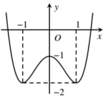
Các câu hỏi tương tự
Cho hàm số
y
f
x
có đồ thị như hình vẽ bên. Tìm giá trị cực đại của hàm số.
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình vẽ bên. Tìm giá trị cực đại của hàm số.
Cho đồ thị hàm số như hình vẽ bên. Giá trị cực đại của hàm số là
Đọc tiếp
Cho đồ thị hàm số như hình vẽ bên. Giá trị cực đại của hàm số là
Đồ thị hàm số có điểm cực tiểu là O(0; 0) và điểm cực đại là M(1; 1). Giá trị của a,b,c,d lần lượt là: A. . B. . C. . D.
Đọc tiếp
Đồ thị hàm số 
có điểm cực tiểu là O(0; 0) và điểm cực đại là M(1; 1). Giá trị của a,b,c,d lần lượt là:
A. 
.
B. 
.
C. 
.
D. 
Cho hàm số
y
f
x
có đồ thị như hình vẽ bên dưới Giá trị cực tiểu của hàm số
y
f
x
bằng A. -1 B. 3 C. 1 D. 2
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình vẽ bên dưới
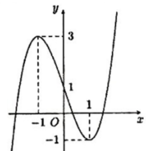
Giá trị cực tiểu của hàm số y = f x bằng
A. -1
B. 3
C. 1
D. 2
Cho hàm số: y
x
3
− (m + 4)
x
2
− 4x + m (1)a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m 0d) Xác định k để (C) cắt đường thẳng y kx tại ba điểm phân biệt.
Đọc tiếp
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m = 0
d) Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
Cho hàm số
y
a
x
4
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a...
Đọc tiếp
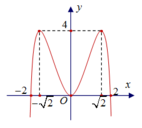
Cho hàm số y = a x 4 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a # 0 có đồ thị như hình vẽ bên.
Các điểm cực tiểu của hàm số là
Cho hàm số
y
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có hai cực trị
x
1
,
x
2
thỏa
-
2
x
1
0
x
2
2...
Đọc tiếp
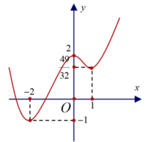
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
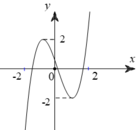
Số điểm cực tiểu của hàm số 
là
A. 3.
B. 5.
C. 7.
D. 4.
Cho hàm số y ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho hàm số y = ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị?
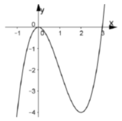
A. 2
B. 3
C. 4
D. 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
a
,
b
,
c
∈
ℝ
có đồ thị như hình vẽ. Số điểm cực trị của hàm số đã cho là
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c a , b , c ∈ ℝ có đồ thị như hình vẽ.
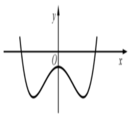
Số điểm cực trị của hàm số đã cho là
