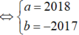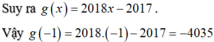Các câu hỏi tương tự
Gọi A là tổng các chữ số của một số có 2018 chữ số, B là tổng các chữ số của A và C là tổng các chữ số của B. Gọi * là giá trị lớn nhất có thể có của C. Lấy số nguyên dương nhỏ nhất chia hết cho 11 và có tích các chữ số bằng (3x * + 2) chia cho 13. Số dư còn lại sau khi chia là **. Tìm * và **.
Cho tứ diện ABCD có M, N, P lần lượt thuộc các cạnh AB, BC, CD sao cho MAMB, NB2NC, PC2PD. Mặt phẳng (MNP) chia tứ diện thành hai phần. Gọi T là tỉ số thể tích của phần nhỏ chia phần lớn. Giá trị của T bằng? A. 13/25 B. 25/43 C. 19/26 D. 26/45
Đọc tiếp
Cho tứ diện ABCD có M, N, P lần lượt thuộc các cạnh AB, BC, CD sao cho MA=MB, NB=2NC, PC=2PD. Mặt phẳng (MNP) chia tứ diện thành hai phần. Gọi T là tỉ số thể tích của phần nhỏ chia phần lớn. Giá trị của T bằng?
A. 13/25
B. 25/43
C. 19/26
D. 26/45
Cho hình chóp tứ giá đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc
60
0
. Gọi M là điểm đối xứng của C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:
Đọc tiếp
Cho hình chóp tứ giá đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 0 . Gọi M là điểm đối xứng của C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:

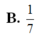
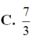
Chia số A cho 4 thì được thương là 215 và còn dư. Chia số A cho 8 thì dư 7. Tìm số A?
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
-
4
x
+
4
trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A(0;4) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là A. K -6 B. K -2 C.K -8 D. K -4
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 4 x + 4 trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A(0;4) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là
A. K = -6
B. K = -2
C.K = -8
D. K = -4
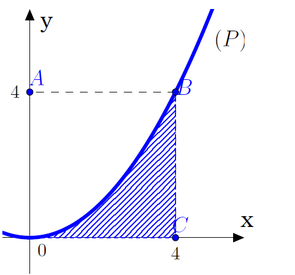
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox. A. . B. . C. . D. .
Đọc tiếp
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox. A. B. C. D.
Đọc tiếp
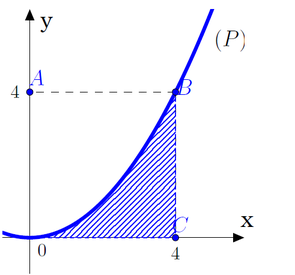
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
Đọc tiếp
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
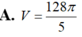
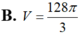
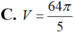
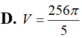
Xét hình phẳng (H) được giới hạn bởi hàm số
y
x
2
, đường thẳng
y
k
2
với
0
≤
k
≤
1
; trục tung và đường thẳng x1. Biết (H) được chia thành hai phần có diện tích
S
1
S
2
như hình vẽ. Gọi...
Đọc tiếp
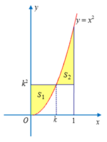
Xét hình phẳng (H) được giới hạn bởi hàm số y = x 2 , đường thẳng y = k 2 với 0 ≤ k ≤ 1 ; trục tung và đường thẳng x=1. Biết (H) được chia thành hai phần có diện tích S 1 S 2 như hình vẽ. Gọi k 1 , k 2 lần lượt là giá trị của k làm cho tổng S 1 + S 2 có giá trị lớn nhất và nhỏ nhất. Tính giá trị của T = k 1 + k 2
![]()