Đáp án D
Hướng dẫn giải:
Y C B T ⇒ ∆ C J D vuông cân tại J
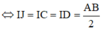
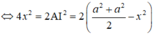
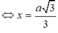
Đáp án D
Hướng dẫn giải:
Y C B T ⇒ ∆ C J D vuông cân tại J
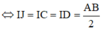
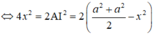
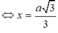
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=a, CD=2x. Tính giá trị của x sao cho hai mặt phẳng (ABC) và (ABD) vuông góc với nhau


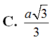
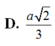
Cho tứ diện ABCD có (ACD) ⊥ (BCD), AC = AD = BC = BD = a, CD = 2x . Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:
A. a 2 3
B. a 3 3
C. a 3 2
D. a 5 3
Cho tứ diện ABCD có AB = AD = a 2 , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A.600
B.450
C.900
D.1200
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tam giác ABC, vuông cân ở A và AB = a. Trên đường thẳng qua C, vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với BD cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau theo giao tuyến ∆ . Trên đường thẳng ∆ lấy hai điểm A, B với AB=a. Trong mặt phẳng (P) lấy điểm C và trong mặt phẳng (Q) lấy điểm D sao cho AC, BD cùng vuông góc với ∆ và AC=BD=AB. Bán kính mặt cầu ngoại tiếp tứ diện ABCD là:
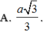
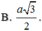
![]()
![]()
Cho tứ diện ABCD có C D = a 2 , ∆ A B C là tam giác đều cạnh a, ∆ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A. 4 πa 3 3
B. πa 3 6
C. 4 πa 3
D. πa 3 3 2
Cho tứ diện ABCD có AB=BC=AC=BD=2a, AD= a 3 ; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt BM=x, DN=y (0<x,y<a). Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là:
![]()
![]()
![]()
![]()