Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'
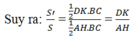
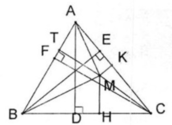
Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'
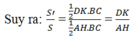

cho tam giác ABC vuông tại A có AB = 15cm, BC = 25cm . AH là đường cao của tam giác ABC .
a. chứng minh tam giác ABC đồng dạng với tam giác BCA
b. tính AC và AH
C. Gọi BF là tia phân giác của tam giác ABC , BF cắt AH tại D.
chứng minh tam giác ABD đồng dạng với tam giác CBF
d. Trên tia đối của tia AB lấy điểm E sao cho AE = 10cm . Qua E vẽ đường thằng D song song BF cắt AC tại K
chứng minh : AK*BH = AE* DH và diện tích của tam giác ABC = 3 phần 5 diện tích của tam giác EBC
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?
Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJ=SABI+SCBJ
Bài 3: Cho tam giác ABC có AB=3cm, BC=4cm, CA=5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tính diện tích mỗi phần?
Bài 4: Cho tam giác ABC có diện tích 30cm2. trên cạnh AB lấy điểm D sao cho AD=2DB, trên cạnh AC lấy điểm E sao cho AE=3EC. Gọi M là giao điểm của BE và CD. Tính diện tích tam giác AMB?
Cho tam giác ABC nhọn có 3 đường cao AD BE CF và trực tâm H. Lấy H' đối xứng với H qua BC. Gọi M N là chân đường vuông góc kẻ từ H' đến AB và AC. a, Chứng minh góc AEF=góc ABC. b, CHỨNG MINH EH là tia phân giác của góc DEF và M D N thẳng hàng. c, Gọi S S1 S2 S3 lần lượt là diện tích của các tam giác ABC AEF BDF CDE, chứng minh S1S2S3/S^3 <= 1/64
cho tam giác ABC vuông tại A, đường cao AH. Gọi E,F thứ tự là hình chiếu của H trên AB, AC
a, Cm tứ giác AEHF là hình chữ nhật
b, Cm BE.HC=AH.EH
c, ký hiệu diện tích tam giác ABC là S(ABC), diện tích hình chữ nhật AEHF là S(AEHF) Chứng minh S(AEHF) \(\le\)S(ABC). Dấu bằng xảy ra khi và chỉ khi tam giác ABC là tam giác vuông cân .
Cho tam giác ABC vuông tại A có AB=15cm , AC=20cm. Kẻ đường cao AH . gọi I và K là hình chiếu của H trên AB , AC .
a) chưng minh AK.AC=HB.HC
b) tính IK
c) tính S tam giác AIK / S tam giác ABC
d) chưng minh IH^3 / IA^3 = IB/KC
Tam giác ABC vuông tại A có AB=24cm, AC=32cm. Kẻ đường cao AH.
a) Tính BC và diện tích ABC
b) Chứng minh tam giác ABH và tam giác ABC đồng dạng. Tính AH, BH, CH và SABH/SABC
c) Vẽ trunng tuyến AM. Tính SAHM
d) Gọi I, K lần lượt là trung điểm BH, CH. Chứng minh tam giác ABI đồng dạng tam giác CAK và AI vuông góc với CK
Giúp mình với... Mai nộp rồi... Nhất là câu d
Cho tam giác ABC, kẻ 3 đường thẳng AM,BN,CP nằm trong tam giác. G là giao điểm của 03 đường thẳng trên. Chứng minh rằng nếu S tam giác GAC= S tam giác GBC= S tam giác GAB (S là diện tích) thì G là trọng tâm của tam giác.
Cho tam giác ABC cân tại A, có diện tích S. Gọi O là trung điểm của đường cao AH. Gọi D là giao điểm của BO với cạnh AC và E là giao điểm của CO với cạnh AB. Tính diện tích tứ giác ADOE theo S
Cho tam giác ABC và tam giác DBC vuông tại A và D ( A và D nằm khác phía so với bờ là đường thẳng BC ). Gọi H,K lần lượt là hình chiếu vuông góc của B và C xuống AD. Chứng minh rằng AH = DK.