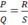 ⇒ PS = QR (1) và P ≠ Q, R ≠ S
⇒ PS = QR (1) và P ≠ Q, R ≠ S
Trừ từng vế đẳng thức (1) với PR: PS – PR = QR – PR
⇒ P(S – R) = R(Q – P) 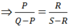
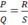 ⇒ PS = QR (1) và P ≠ Q, R ≠ S
⇒ PS = QR (1) và P ≠ Q, R ≠ S
Trừ từng vế đẳng thức (1) với PR: PS – PR = QR – PR
⇒ P(S – R) = R(Q – P) 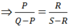
Cho hai phân thức \(\frac{P}{Q}\)và \(\frac{R}{S}\). Chứng tỏ rằng :
a) Nếu \(\frac{P}{Q}=\frac{R}{S}\)thì \(\frac{P+Q}{Q}=\frac{R+S}{S};\)
b) Nếu \(\frac{P}{Q}=\frac{R}{S}\)và \(P\ne Q\)thì \(R\ne S\)và \(\frac{P}{Q-P}=\frac{R}{S-R}.\)
Cô ơi, cô đừng giải nhe cô, mà cô hướng dẫn giúp em phương pháp chi tiết, dể hiểu và sử dụng các tính chất, công thức nào để giải từng câu a) và câu b) nhe cô, em cám ơn cô nhiều ạ ? ^^
1. trong mỗi trường hợp sau tìm hai đa thức P và Q thõa mãn đẳng thức
a)\(\frac{\left(x+2\right)P}{x-2}=\frac{\left(x-1\right)Q}{x^2-4}\)
b)\(\frac{\left(x+2\right)P}{x^2-1}=\frac{\left(x-2\right)Q}{x^2-2x+1}\)
2, cho hai phân thức \(\frac{P}{Q}\)và \(\frac{R}{S}\). chứng tỏ rằng:
a) nếu\(\frac{P}{Q}=\frac{R}{S}\) thì \(\frac{P+Q}{Q}=\frac{R+S}{S}\)
b) nếu\(\frac{P}{Q}=\frac{R}{S}\) và\(P\ne Q\) thì\(R\ne S\) và\(\frac{P}{Q-P}=\frac{R}{S-R}\)
Cho hai phân thức \(\frac{P}{Q}\)và \(\frac{R}{S}.\)Chứng tõ rằng :
Nếu \(\frac{P}{Q}=\frac{R}{S}\)và \(P\ne Q\)và \(R\ne S\)thì \(\frac{P}{Q-P}=\frac{R}{S-R}.\)
Cô ơi, người ta cho mình 2 điều kiện là : \(P\ne Q,R\ne S.\)để làm gì vậy cô ? Cô ơi, cô giải thích chi tiết và ví dụ vào bài này luôn giúp em nhe cô. Em cám ơn cô ạ. ^^
Cho hai phân thức P Q và R S thỏa mãn P Q = R S và P ≠ Q.
Chứng minh: R ≠ S và P Q + P = R S + R .
cho hai phan thức \(\frac{P}{Q}\) và\(\frac{R}{S}\) chứng to rằng
Câu (a) \(\frac{P}{Q}\)=\(\frac{R}{S}\) thì\(\frac{P+Q}{Q}\)=\(\frac{R+S}{S}\)
Câu(b) \(\frac{P}{Q}\)=\(\frac{R}{S}\) thì P khác S thì R khác S và \(\frac{P}{Q-P}\)=\(\frac{R}{S-R}\)
cmr nếu các số nguyên dương a,b,p,q,r,s thỏa mãn các điều kiện :
qr - ps = 1 và p/q < a/b < r/s thì b > hoặc = q + s
mấy cậu giải thích rõ nhé ( cảm ơn )
B1. Cho f(1)=1008,f(1)+f(2)+...+f(n)=n^2.f(n) f(n)la ham so duong
tinh f(2015)
B2 Cho cac so nguyen to q,p,r,s sao cho cac so sau deu la so nguyen to p^s+s^q,q^s+s^r,r^s+s^p
tim cac so p,q,r,s
B3 co a,b,c duong a mu 3+bmu3=c^3
so sanh a^2015+b^2015 va c^2015
Cho hai phân thức P Q v à R S
Chứng minh rằng :
Nếu P Q = R S thì P + Q Q = R + S S
Cho tứ giác ABCD. Gọi P,Q,R,S lần lượt là trung điểm của AB,BC,CD,DA.
a) chứng minh PQRS là hình bình hành
b) Nếu ABCD là hình thang cân thì PQRS là hình gì ? Chứng minh
c) Nếu ABCD là hình vuông thì PQRS là hình gì ? Chứng minh