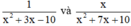Thật vậy, ta có:
x3 + 5x2 – 4x – 20
= x3 + 3x2 – 10x + 2x2 + 6x – 20
= x(x2 + 3x – 10) + 2(x2 + 3x – 10)
= (x + 2)(x2 + 3x – 10)
⇒ x3 + 5x2 – 4x – 20 chia hết cho x2 + 3x – 10
x3 + 5x2 – 4x – 20
= x3 + 7x2 + 10x – 2x2 – 14x – 20
= x(x2 + 7x + 10) – 2.(x2 + 7x + 10)
= (x – 2)(x2 + 7x + 10)
⇒ x3 + 5x2 – 4x – 20 chia hết cho x2 + 7x + 10
Do đó có thể chọn mẫu thức chung là x3 + 5x2 – 4x – 20.
Cho hai phân thức 1 x 2 - 4 x - 5 ; 2 x 2 - 2 x - 3 Chứng tỏ rằng có thể chọn đa thức x 3 - 7 x 2 + 7 x + 15 làm mẫu thức chung để quy đồng mẫu thức của hai phân thức đã cho. Hãy quy đồng mẫu thức.
cho hai phân thức \(\frac{1}{x^2-4x-5}\) và \(\frac{2}{x^2+3x-10}\)
chứng tỏ rằng có thể chọn đa thức x3-7x2+7x+15 làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.Hãy quy đồng mẫu thức
Cho hai phân thức: \(\frac{1}{x^2-4x-5}\) và \(\frac{2}{x^2-2x-3}\)
Chứng tỏ rằng có thể chọn đa thức \(x^3-7x^2+7x+15\)làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức
Cho các phân thức 1 a 2 − a − 2 và a a 2 + 3 a + 2 với a ≠ ± 2 và a ≠ − 1 .
Không dùng các phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là
Cho các phân thức x − 3 2 x 2 − 3 x − 2 và 2 x − 1 x 2 + x − 6 với x ≠ − 3 ; x ≠ − 1 2 và x ≠ 2 . Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là N = 2 x 3 + 3 x 2 − 11 x − 6 .
Cho hai phân thức:\(\frac{1}{x^2+3x-10}\); \(\frac{x}{x^2+7x+10}\)
Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là \(x^3+5^2-4x-20\)
Cho hai phân thức 1 x 2 + ax − 2 và 2 x 2 + 4 x − b , với x ≠ − 3 ; x ≠ − 1 và x ≠ 2 .
a) Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là A = x 3 + 2 x 2 − 5 x − 6 ;
b) Với a và b tìm được hãy viết hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là A = x 3 + 2 x 2 − 5 x − 6 .
Cho hai phân thức 1 x 2 + a x - 2 và 2 x 2 + 5 x + b . Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là x 3 + 4 x 2 + x - 6 . Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là x 3 + 4 x 2 + x - 6
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
x 2 - y 2 x + y 6 x - 6 y
