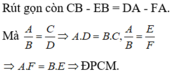Các câu hỏi tương tự
Có bao nhiêu bộ số nguyên dương (a,b,c,d,e,f) thỏa mãn a>b≥ c≥ d≥ e≥ f và phương trình a!=b!+c!+d!+e!+f!?
cho a,b,c,d,e,f thuộc N*
a/b>c/d>e/f và af-be=1. chứng minh rằng d>b+f
a) chứng minh: A'B'C' đồng dạng D'E'F'
b) chứng minh: B'C'.D'F'=A'C'.E'F'
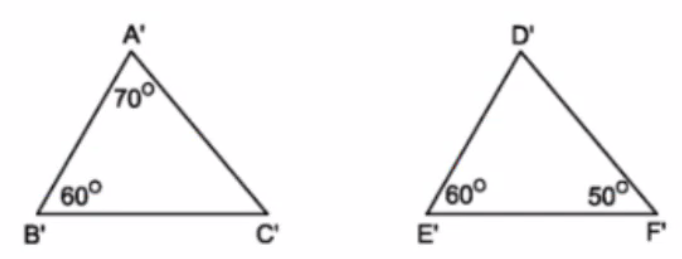
a) chứng minh: A'B'C' đồng dạng D'E'F'
b) chứng minh: B'C'.D'F'=A'C'.E'F'
Cho các số thực dương a,b,c,d,e,f thoả mãn \(a+b+c+d+e+f=6\)và \(abc+def\ge2.\)Chứng minh rằng: \(ace+afe+cde+abf+bcd+bdf\le6.\)
1,tập hợp các số 1,2,3,...100 được chia thành 7 tập hợp con(mỗi tập có ít nhất 1 phân tử ).chứng minh rằng ít nhất ở một trong các tập con ấy tìm được 4 số a,b,c,d sao cho a+b=c+d hoặc 3 số e,f ,g sao cho e+f=2g
2,Cho P(x) là một đa thức bậc hai thỏa mãn x^2-2x+2<=P(x)<=2x^2-4x+3 với mọi giá trị của x và P(x)=181.tính P(2016)
Cho hình thang ABCD (AB//CD) với AB a, BC b, CD c và DA d. Các tia phân giác của góc A và góc D cắt nhau tại E, các tia phân giác của
B
^
và
C
^
cắt nhau tại F. Gọi M, N theo thứ tự là trung điểm của AD và BC.a) Chứng minh M, E, N, F cùng nằm trên một đường thẳng.b) Tính độ dài MN, MF, FN theo a, b, c, d.
Đọc tiếp
Cho hình thang ABCD (AB//CD) với AB = a, BC = b, CD = c và DA = d. Các tia phân giác của góc A và góc D cắt nhau tại E, các tia phân giác của B ^ và C ^ cắt nhau tại F. Gọi M, N theo thứ tự là trung điểm của AD và BC.
a) Chứng minh M, E, N, F cùng nằm trên một đường thẳng.
b) Tính độ dài MN, MF, FN theo a, b, c, d.
Cho a+b = c+d = e+f , với a,b,c,d,e,f là số nguyên tố phân biệt, nhỏ hơn 20.Tìm a+b
Cho hình thang ABCD (AB // CD) với AB = a, BC = b, CD = c, DA = d. Các tia
phân giác của góc A và góc D cắt nhau tại E, các tia phân giác của góc B và góc C cắt nhau
tại F. Gọi M, N theo thứ tự là trung điểm của AD và BC.
a) Chứng minh M, E, F, N thẳng hàng.
b) Tính độ dài MN, MF, FN theo a, b, c, d.
Cho
a/b + c/d + e/f = 1
b/a +d/c +f/e = 1
chứng minh
A2/b2 + c2/d2 +e2/f2 = 1