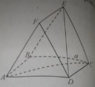
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A, B, C, D.a) Tứ giác A, B, C, D là hình gì? Chứng minh rằng .b) Chứng minh rằng điều kiện để tứ giác A, B, C, D là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).c) Chứng minh rằng điều kiện để tứ giác A, B, C, D là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Đọc tiếp
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).