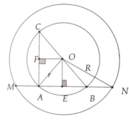
Kẻ OE ⊥ AB; OF ⊥ AC
Đặt AC=a, AM=b, AN=c
r 2 = a 2 2 + c - b 2 2
R 2 = a 2 2 + c + b 2 2
Ta chứng minh được: a 2 + b 2 + c 2 = 2 R 2 + r 2

Kẻ OE ⊥ AB; OF ⊥ AC
Đặt AC=a, AM=b, AN=c
r 2 = a 2 2 + c - b 2 2
R 2 = a 2 2 + c + b 2 2
Ta chứng minh được: a 2 + b 2 + c 2 = 2 R 2 + r 2
Cho 2 đường tròn đồng tâm O có bán kính R và r \(\left(R>r\right)\). A và M là 2 điểm thuộc đường tròn nhỏ. Qua M kẻ dây BC của đường tròn lớn sao cho \(BC\perp AM\). Tính \(MA^2+MB^2+MC^2\)theo R và r.
Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Vẽ tiếp tuyến AM,AN với đường tròn tâm O . Đường thẳng chứa đường kính của đường tròn song song với MN cắt AM tại B và cắt AN tại C .
a, Gọi I là giao điểm của AC và đường tròn tâm O. CMR: I là tâm đường tròn nội tiếp tam giác AMN
b,CM tứ giác MNCB là hình thang cân
c, CM: MA.MB=R2
d, Lấy D thuộc cung nhỏ MN vẽ tiếp tuyến đường tròn tâm O qua D cắt AM,AN lần lượt tại P và Q . CM: BP.CQ=BC2/4
Cho đường tròn tâm O, bán kính R và một điểm A sao cho OA=2R. VẼ các tiếp tuyến AB,AC ( B,C) là các tiếp điểm. Đường thẳng OA cắt BC tại H, cắt cung nhỏ BC và cung lớn BC lần lượt tại I,K
a/ CM OA vuông góc với BC, HI=OA=R bình phương
b/ CM tam gaics ABC đều, tứ giác ABKC là hình thoi
c/ CHứng tỏ I là tâm đường tròn nội tiếp tam giác ABC. Tính theo R bán kính của đường tròn này.
d/ Vẽ cát tueyens bất kì AMN của đường tròn tâm O. Gọi E là tủng điểm MN. CHứng tỏ 5 điểm O,E,A,B,C cùng thuộc một đường tròn
Cho 2 đường tròn đồng tâm O có bán kính R và r (R>r).A,M là 2 điểm thuộc đường tròn nhỏ (A di động,M cố định).Qua M vẽ dây BC của đường tròn lớn sao cho BC\(\perp\)AM.
a) Chứng minh tổng \(MA^2+MB^2+MC^2\) không phụ thuộc vào A
b) chứng minh trọng tâm G của tam giác ABC cố định
Cho 2 đường tròn đồng tâm O có bán kính R và r (R>r).A,M là 2 điểm thuộc đường tròn nhỏ (A di động,M cố định).Qua M vẽ dây BC của đường tròn lớn sao cho BC⊥⊥AM.
a) Chứng minh tổng \(MA^2+MB^2+MC^2\) không phụ thuộc vào A
b) chứng minh trọng tâm G của tam giác ABC cố định
CHO ĐƯỜNG TRÒN TÂM 0 BÁN KÍNH r, ĐƯỜNG KÍNH CD, vẽ đường tròn tâm O' có bán kính nhỏ hơn R cắt CD tại P và Q.Từ P và Q lần lượt vẽ 2 đường thẳng song song với nhau cắt đường tròn tâm O bãn kính R tại N và M. Tính diện tích tứ giác MNPQ
biết R-13,MN=10
Hộ mk vs cảm ơn mn
Cho đường tròn tâm O bán kính R có đường kính AB cố định. Vẽ đường kính MN của đường tròn tâm O bán kính R (M khác A ,M khác B). Tiếp tuyến của dường tròn tâm o bán kính r tại B cắt đường thẳng AM AN lần lượt tại Q và P
a, Cm tg AMNB Là hình chữ nhật
b, chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
Cho đường tròn tâm O, bán kính R. Điểm A thuộc đường tròn, BC là một đường kính (A khác B và C) . Vẽ AH vuông góc với BC tại H. Gọi E, M lần lượt là trung điểm của AB, AH và P là giao điểm của OE với tiếp tuyến tại A của (O ; R).
a) CMR: AB2 = BH.BC
b) CM: PB là tiếp tuyến của đường tròn (O)
c) CM: 3 điểm P, M, C thẳng hàng
d) Gọi Q là giao điểm của đường thẳng PA với tiếp tuyến tại C của đường tròn (O). Khi A thay đổi trên đường tròn (O), tìm giá trị nhỏ nhất của tổng OP + OQ
Cho đường tròn tâm O, bán kính R. Điểm A thuộc đường tròn, BC là một đường kính (A khác B và C) . Vẽ AH vuông góc với BC tại H. Gọi E, M lần lượt là trung điểm của AB, AH và P là giao điểm của OE với tiếp tuyến tại A của (O ; R).
a) CMR: AB2 = BH.BC
b) CM: PB là tiếp tuyến của đường tròn (O)
c) CM: 3 điểm P, M, C thẳng hàng
d) Gọi Q là giao điểm của đường thẳng PA với tiếp tuyến tại C của đường tròn (O). Khi A thay đổi trên đường tròn (O), tìm giá trị nhỏ nhất của tổng OP + OQ