Các câu hỏi tương tự
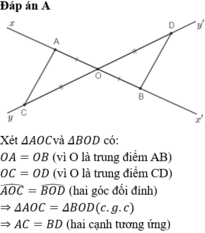
Cho 2 đường thẳng xx' và yy' cắt nhau tại O , Trên xx' lấy A và B sao cho 0 là trung điểm AB . Trên yy' lấy C và D sao cho O là trung điểm CD
CMR : AC//BD
Ai đúng mik tickk nhó
Cho hai đường thẳng xx ,yy cắt nhau tại O. Trên xx lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy lấy C,D sao cho O là trung điểm CD
(
A
∈
O
x
;
C
∈
O
y
)
Chọn câu đúng A.
Δ
A
O
C
Δ
B
D
O
B.
Δ
A
O
D
Δ
C
O
B
C. ...
Đọc tiếp
Cho hai đường thẳng xx' ,yy' cắt nhau tại O. Trên xx' lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy' lấy C,D sao cho O là trung điểm CD ( A ∈ O x ; C ∈ O y )
Chọn câu đúng
A. Δ A O C = Δ B D O
B. Δ A O D = Δ C O B
C. Δ A O C = Δ B O D
D. O A C ^ = O D B ^
Cho xx'//yy' , lấy A thuộc xx' , B thuộc yy' . Gọi M là trung điểm AB . Qua M vẽ đường thẳng d cắt xx' tại C và yy' tại D
CMR : AC=BD
Cho 2 đường thẳng xx', yy' cắt nhau tại O. Trên tia Ox và Ox' lần lượt lấy các điểm A và C, trên Oy và Oy' lần lượt các điểm B và D sao cho OA=OB; OC=OD. Gọi M,N lần lượt là trung điểm của AB và BD. Chứng minh M,O,N thẳng hàng
Cho đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đường. Chứng minh a)∆AOD ∆BOC b)AC // BD và AC BD c)CB // AD và AD BCd)Lấy điểm I thuộc AD, K thuộc BC sao co AI BK. Chứng minh rằng: O là trung điểm IK
Đọc tiếp
Cho đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đường. Chứng minh
a)∆AOD = ∆BOC
b)AC // BD và AC = BD
c)CB // AD và AD = BC
d)Lấy điểm I thuộc AD, K thuộc BC sao co AI = BK. Chứng minh rằng: O là trung điểm IK
Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Chứng minh 3 điểm M,C,N thẳng hàng
Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia đối của tia AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Cm: Ba điểm M,C,N thẳng hàng
Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia đối của tia AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Cm: Ba điểm M,C,N thẳng hàng
(^-^)CẦN GIẢI GẤP ĐỐNG BÀI NÀY(Có cả hình ở mỗi bài nha!)Câu 1: Cho tam giác ABC có AB AC. Kẻ BD vuông góc với AC (D∈AC),CE vuông góc với AB ( E ∈ AB ). Gọi O là giao điểm của BD và CE. Chứng minh : a) BD CEb) Tam giác OEB bằng tam giác ODCc) AO là tia phân giác của góc BACd) Gọi M là trung điểm của BC. Chứng minh : A,O,M thẳng hàng.Câu 2 :Câu 3 :Cho tam giác ABC có ACAB. Nối A với trung điểm M của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của AE, Nối C với E. a) So sánh AB và CEb) C...
Đọc tiếp
(^-^'')
CẦN GIẢI GẤP ĐỐNG BÀI NÀY
(Có cả hình ở mỗi bài nha!)
Câu 1: Cho tam giác ABC có AB = AC. Kẻ BD vuông góc với AC (D∈AC),CE vuông góc với AB ( E ∈ AB ). Gọi O là giao điểm của BD và CE. Chứng minh :
a) BD = CE
b) Tam giác OEB bằng tam giác ODC
c) AO là tia phân giác của góc BAC
d) Gọi M là trung điểm của BC. Chứng minh : A,O,M thẳng hàng.
Câu 2 :
Câu 3 :Cho tam giác ABC có AC>AB. Nối A với trung điểm M của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của AE, Nối C với E.
a) So sánh AB và CE
b) Chứng minh : \(\frac{AC-AB}{2}< AM< \frac{AC+AB}{2}.\)
Câu 4: Cho ∆ABC vuông tại C có góc A = 60o. Tia phân giác của góc BAC cắt BC ở E. Kẻ EK ⊥ AB( K ∈ AB ).Kẻ BD ⊥ AE( D ∈ AE ). Chứng minh:
a) AC=AK và AE ⊥ CK
b) KA=KB
c) EB>AC
d) Ba đường thẳng AC,BD,KE đồng quy.
Câu 5: Cho ∆ABC có AB<AC. Trên cạnh AC lấy điểm D sao cho CD=AB. Hai đường trung trực của BD và AC cắt nhau tại E. Chứng minh rằng:
a)∆AEB = ∆CED
b) AE là tia phân giác trong tại đỉnh A của ∆ABC