Các câu hỏi tương tự
Cho A, B là hai điểm biểu diễn hình học số phức theo thứ tự
z
0
,
z
1
khác 0 và thỏa mãn đẳng thức
z
0
1
+
z
1
2
z
0
.
z
1
. Hỏi ba điểm O, A, B tạo thành tam gi...
Đọc tiếp
Cho A, B là hai điểm biểu diễn hình học số phức theo thứ tự z 0 , z 1 khác 0 và thỏa mãn đẳng thức z 0 1 + z 1 2 = z 0 . z 1 . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
A. cân tại O.
B. Vuông cân tại O.
C. đều.
D. Vuông tại O.
Gọi A, B là hai điểm trong mặt phẳng phức theo thứ tự biểu diễn các số phức
z
1
,
z
2
khác 0 thỏa mãn đẳng thức
z
1
2
+
z
2
2
-
z
1
z
2
0, khi đó tam giác OAB (O là gốc...
Đọc tiếp
Gọi A, B là hai điểm trong mặt phẳng phức theo thứ tự biểu diễn các số phức z 1 , z 2 khác 0 thỏa mãn đẳng thức z 1 2 + z 2 2 - z 1 z 2 = 0, khi đó tam giác OAB (O là gốc tọa độ)
A. Là tam giác đều.
B. Là tam giác vuông.
C. Là tam giác cân, không đều.
D. Là tam giác tù.
Cho A và B theo thứ tự là các điểm biểu diễn các số phức
z
1
và
z
2
. Biết
z
1
z
¯
2
≠
0
. Mệnh đề nào dưới đây đúng? A. A và B đối xứng qua trục Ox. B. A và B đối xứng qua trục Oy. C. A và B đối xứng qua gốc tọa độ O. D. A và B đối xứng qua đường thẳng yx.
Đọc tiếp
Cho A và B theo thứ tự là các điểm biểu diễn các số phức z 1 và z 2 . Biết z 1 = z ¯ 2 ≠ 0 . Mệnh đề nào dưới đây đúng?
A. A và B đối xứng qua trục Ox.
B. A và B đối xứng qua trục Oy.
C. A và B đối xứng qua gốc tọa độ O.
D. A và B đối xứng qua đường thẳng y=x.
Cho các số phức
z
1
,
z
2
với
z
1
≠
0. Tập hợp các điểm biểu diễn số phức w
z
1
.
z
+
z
2
là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các điểm biểu diễn số phức z là đường nào sau đây? A. đường tròn tâm là gốc...
Đọc tiếp
Cho các số phức z 1 , z 2 với z 1 ≠ 0. Tập hợp các điểm biểu diễn số phức w = z 1 . z + z 2 là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các điểm biểu diễn số phức z là đường nào sau đây?
A. đường tròn tâm là gốc tọa độ, bán kính bằng | z 1 |
B. đường tròn tâm là điểm biểu diễn số phức - z 2 z 1 , bán kính bằng 1 | z 1 |
C. đường tròn tâm là gốc tọa độ, bán kính bằng 1 | z 1 |
D. đường tròn tâm là điểm biểu diễn số phức z 2 z 1 bán kính bằng 1 | z 1 |
Cho
z
1
,
z
2
là hai trong các số phức z thỏa mãn điều kiện |z - 5 – 3i| 5, đồng thời
z
1
-
z
2
0
. Tập hợp các điểm biểu diễn của số phức
w
...
Đọc tiếp
Cho z 1 , z 2 là hai trong các số phức z thỏa mãn điều kiện |z - 5 – 3i| = 5, đồng thời z 1 - z 2 = 0 . Tập hợp các điểm biểu diễn của số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình nào dưới đây?
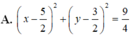
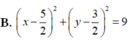
![]()
![]()
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
;
z
2
2
+
i
;
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
![]()
![]()
![]()
![]()
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
,
z
2
2
+
i
,
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành A. z -3 - i B. z -2 – i C. z -1 –...
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i , z 2 = 2 + i , z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 – i
C. z = -1 – 3i
D. z = -3
Gọi điểm A,B lần lượt biểu diễn các số phức z và
z
1
+
i
2
z
;
(z khác 0) trên mặt phẳng tọa độ (A,B,C và A,B,C đều không thẳng hàng). Với O là gốc tọa độ, khẳng định nào sau đây đúng? A. Tam giác OAB đều B. Tam giác OAB vuông cân tại O C. Tam giác OAB vuông cân tại B D. Tam giác OAB vuông cân tại A
Đọc tiếp
Gọi điểm A,B lần lượt biểu diễn các số phức z và z ' = 1 + i 2 z ; (z khác 0) trên mặt phẳng tọa độ (A,B,C và A',B',C' đều không thẳng hàng). Với O là gốc tọa độ, khẳng định nào sau đây đúng?
A. Tam giác OAB đều
B. Tam giác OAB vuông cân tại O
C. Tam giác OAB vuông cân tại B
D. Tam giác OAB vuông cân tại A
Gọi S là tập hợp tất cả các số thực a sao cho phương trình
z
2
+
a
-
2
z
+
2
a
-
3
0
có hai nghiệm phức
z
1
;
z
2
và các điểm biểu diễn của
z
1
;
z
2...
Đọc tiếp
Gọi S là tập hợp tất cả các số thực a sao cho phương trình z 2 + a - 2 z + 2 a - 3 = 0 có hai nghiệm phức z 1 ; z 2 và các điểm biểu diễn của z 1 ; z 2 cùng với gốc tọa độ O tạo thành một tam giác đều. Tổng các phần tử của S bằng
A. 12
B. 11,5
C. 13,5
D. 10





