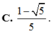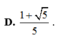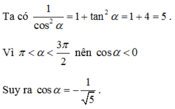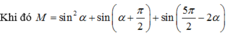Các câu hỏi tương tự
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Cho góc
α
thỏa mãn điều kiện
π
α
3
π
2
và tan
α
2
Tính giá trị của biểu thức
M
sin
2
α
+
sin
α
+
π
2
+
sin...
Đọc tiếp
Cho góc α thỏa mãn điều kiện π < α < 3 π 2 và tan α = 2
Tính giá trị của biểu thức M = sin 2 α + sin α + π 2 + sin 5 π 2 - 2 α
Cho góc
α
thỏa mãn
π
α
3
π
2
và sin
α
-2cos
α
1.Tính A 2tan
α
-cot
α
A. 6 B.
1
6
C. 2 D.
1
2
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và sin α -2cos α =1.Tính A= 2tan α -cot α
A. 6
B. 1 6
C. 2
D. 1 2
Cho góc
α
thỏa mãn:
cos
α
3
5
v
à
-
π
α
0
.Tính giá trị biểu thức:
A
sin
2
α
-
cos
2
α
A.
-
26
25
B....
Đọc tiếp
Cho góc α thỏa mãn: cos α = 3 5 v à - π < α < 0 .Tính giá trị biểu thức: A = sin 2 α - cos 2 α
A. - 26 25
B. - 13 25
C. 3 25
D. - 17 25
Cho góc
α
thỏa mãn:
π
2
α
π
và
sin
α
+
π
.Tính
tan
7
π
3
-
α
A.
3...
Đọc tiếp
Cho góc α thỏa mãn: π 2 < α < π và sin α + π .Tính tan 7 π 3 - α
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho góc
α
thỏa mãn
π
2
α
π
và
sin
α
+
π
-
1
3
. Tính
tan
7
π
2...
Đọc tiếp
Cho góc α thỏa mãn π 2 < α < π và sin α + π = - 1 3 . Tính tan 7 π 2 - α
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho dãy số
(
b
n
)
có số hạng tổng quát là
b
n
sin
α
+
sin
2
α
+
.
.
.
+
sin
n
α
với
α
≠
...
Đọc tiếp
Cho dãy số ( b n ) có số hạng tổng quát là b n = sin α + sin 2 α + . . . + sin n α với α ≠ π / 2 + k π . Tìm giới hạn của ( b n )
Cho góc
α
thỏa mãn
π
α
3
π
2
và
sinα
-
2
cosα
1
Tính A
2
tan
α
-
c
o
t
α
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và sinα - 2 cosα = 1
Tính A= 2 tan α - c o t α
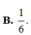
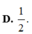
Cho góc
α
thỏa mãn:
π
α
3
π
2
và
A
sin
2
α
+
cos
α
+
π
2
Đọc tiếp
Cho góc α thỏa mãn: π < α < 3 π 2 và A = sin 2 α + cos α + π 2
