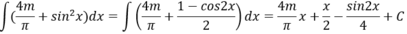
Vì F(0) = 1 nên C =1
F π 4 = π 8 nên tính được m = -3/4
Chọn A.
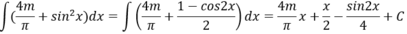
Vì F(0) = 1 nên C =1
F π 4 = π 8 nên tính được m = -3/4
Chọn A.
Tìm nguyên hàm F(x) của hàm số f x = sin ( π - 2 x ) thỏa mãn F ( x 2 ) = 1
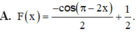
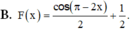
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Cho hàm số f(x)>0 có đạo hàm liên tục trên 0 ; π / 3 , đồng thời thỏa mãn f'(0) = 0; f(0) = 1 và f ' ' x . f x + f x cosx 2 = f ' x 2 .Tính T = f π / 3
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

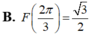
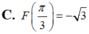
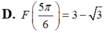
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
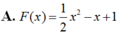
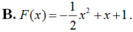
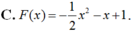
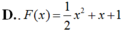
Cho hàm số f(x) có đạo hàm liên tục trên đoạn 0 ; π thỏa mãn: ∫ 0 π f ' x d x = ∫ 0 π cos x . f x d x = π / 2 và f π / 2 = 1 . Khi đó tích phân ∫ 0 π / 2 f x d x bằng
A.0.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) có đạo hàm liên tục trên 0 ; π . Biết f 0 = 2 e và f(x) luôn thỏa mãn đẳng thức f ' x + sinx . f x = cosx . e cosx , ∀ x ∈ 0 ; π . Tính I = ∫ 0 π f x dx (làm tròn đến phần trăm).
A. I ≈ 6,55
B. I ≈ 17,30
C. I ≈ 10,31
D. I ≈ 16,91
Cho hàm số f(x) xác định trên ℝ \ - 2 ; 1 thỏa mãn f ' ( x ) = 1 x 2 + x - 2 ; f ( 0 ) = 1 3 và f(3)-f(-3) = 0 Tính giá trị của biểu thức T = f(-4)+f(-1)-f(4)
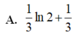
![]()
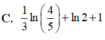
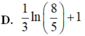
Biết luôn có hai số a, b để F ( x ) = a x + b x + 4 ( 4 a - b ≠ 0 ) là nguyên hàm của hàm số f(x) và thỏa mãn 2 f 2 ( x ) = ( F ( x ) - 1 ) f ' ( x ) . Khẳng định nào dưới đây đúng và đầy đủ nhất?
![]()
![]()
![]()
![]()
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
![]()
![]()
![]()
![]()