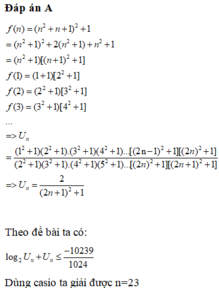Các câu hỏi tương tự
Cho
f
(
n
)
(
n
2
+
n
+
1
)
2
∀
n
∈
N
*
Đặt
u
n
f
(...
Đọc tiếp
Cho f ( n ) = ( n 2 + n + 1 ) 2 ∀ n ∈ N * Đặt u n = f ( 1 ) . f ( 3 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . . . f ( 2 n ) .
Tìm số n nguyên dương nhỏ nhất sao cho u n thỏa mãn điều kiện log 2 u n + u n < - 10239 1024 .
A. n=23
B. n=29
C. n=21
D. n=33
Cho hàm số
f
(
x
)
e
1
+
1
x
2
+
1
(
x
+...
Đọc tiếp
Cho hàm số f ( x ) = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f ( 1 ) . f ( 2 ) . f ( 3 ) . . . f ( 2017 ) = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m - n 2
A. m - n 2 = 2018
B. m - n 2 = 1
C. m - n 2 = -2018
D. m - n 2 = -1
Cho hàm số f(x) có
f
(
1
)
1
,
f
(
m
+
n
)
f
(
m
)
+
f
(
n
)
+
m
n
,
∀
m
,
n
∈
ℕ
*
.
Giá trị của biểu thức
T
log
f
(...
Đọc tiếp
Cho hàm số f(x) có f ( 1 ) = 1 , f ( m + n ) = f ( m ) + f ( n ) + m n , ∀ m , n ∈ ℕ * . Giá trị của biểu thức T = log f ( 96 ) − f ( 69 ) − 241 2 là
A. 4
B. 3
C. 6
D. 9
Cho f(x) = 1^4 +2^4+.....+n^4. Tìm f(x) bậc 5 sao cho f(x+1) - f(x) = x^4
Cho hàm số
f
(
x
)
ln
(
1
-
4
(
2
x
-
1
)
2
)
. Biết rằng
f
(
2
)
+
f
(
3
)
+
.
.
.
+
f
(...
Đọc tiếp
Cho hàm số f ( x ) = ln ( 1 - 4 ( 2 x - 1 ) 2 ) . Biết rằng f ( 2 ) + f ( 3 ) + . . . + f ( 2020 ) = ln a b , trong đó a b là phân số tối giản, a , b ∈ N * . Tính b -3a
A. -2
B. 3
C. -1
D. 1
Cho f(1) 1; f(m + n) f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức
T
log
f
2017
-
f
2016
-
17
2
là A. 3 B. 4 C. 6 D. 9
Đọc tiếp
Cho f(1) = 1; f(m + n) = f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức T = log f 2017 - f 2016 - 17 2 là
A. 3
B. 4
C. 6
D. 9
Cho hàm số
f
(
x
)
1
2
log
2
(
2
x
1
-
x
)
và hai số thực m, n thuộc khoảng (0; 1) sao cho m +n 1. Tính f(m) + f(n). A. 2 B. 0 C. 1 D.
1
2
Đọc tiếp
Cho hàm số f ( x ) = 1 2 log 2 ( 2 x 1 - x ) và hai số thực m, n thuộc khoảng (0; 1) sao cho m +n = 1. Tính f(m) + f(n).
A. 2
B. 0
C. 1
D. 1 2
Cho hàm số
f
(
x
)
1
2
log
2
2
x
1
-
x
và hai số thực m, n thuộc khoảng (0;1) sao cho
m
+
n
1
. Tính
f
(
m
)
+
f
(
n...
Đọc tiếp
Cho hàm số f ( x ) = 1 2 log 2 2 x 1 - x và hai số thực m, n thuộc khoảng (0;1) sao cho m + n = 1 . Tính f ( m ) + f ( n )
A. 2
B. 0
C. 1
D. 1 2
Gọi a là giá trị nhỏ nhất của
f
(
n
)
(
log
3
2
)
log
3
3
log
3
4
....
Đọc tiếp
Gọi a là giá trị nhỏ nhất của f ( n ) = ( log 3 2 ) log 3 3 log 3 4 . . . log 3 n 9 n , với n ∈ N , n ⩾ 2 . Có bao nhiêu số n để f ( n ) = a ?
A. 2
B. Vô số.
C. 1.
D. 4