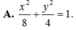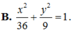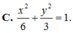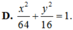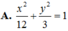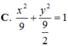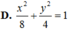Các bài toán về elip chủ yếu qui về việc viết phương trình chính tắc của elip, xác định các phần tử của elip (tâm, đỉnh, tiêu cự, độ dài trục lớn, trục nhỏ, tiêu điểm…). Nhất là xác định phương trình của tiếp tuyến cùng với tọa độ tiếp điểm. Trong mọi trường hợp ta cần nắm vững kiến thức cơ bản sau đây:
Phương trình chính tắcTiêu cựTiêu điểmTrục lớnTrục nhỏĐỉnh trên trục lớnĐỉnh trên trục nhỏTâm saiBán kính qua tiêu điểm của M thuộc EĐường chuẩnCác kiến thức trên được tổng hợp vào bảng sau:

Để giải quyết tốt các lớp bài toán liên quan tới Elip (tìm điểm và viết phương trình tắc của elip) trước tiên chúng ta cần nắm được các kiến thức cơ bản qua sơ đồ sau:
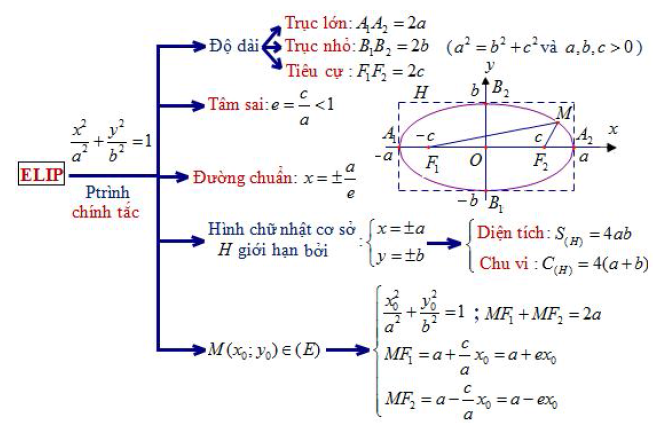
dựa trên các kiến thức cơ bản liên quan tới elip và tính đối xứng của elip (elip nhận hai trục tọa độ làm hai trục đối xứng và gốc tọa độ làm tâm đối xứng).