9.
a. Đúng
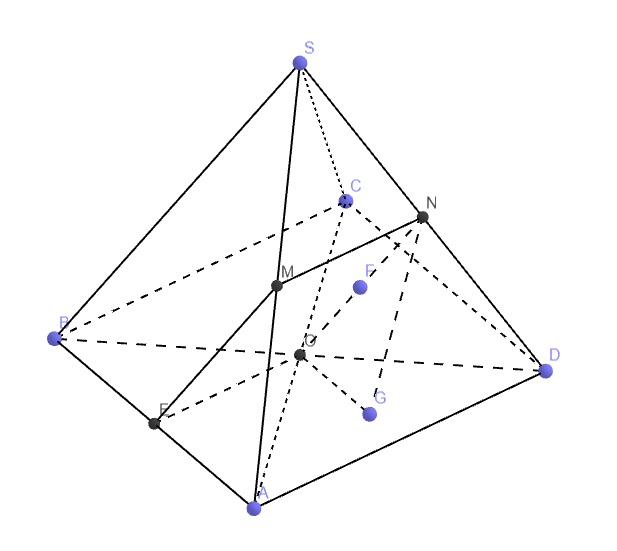
M là trung điểm SA, N là trung điểm SD nên MN là đường trung bình tam giác SAD
\(\Rightarrow MN||AD\Rightarrow MN||BC\) (do \(AD||BC\))
\(\Rightarrow MN||\left(SBC\right)\) (1)
b. Đúng
O là tâm đáy nên O là trung điểm AC
\(\Rightarrow OM\) là đường trung bình tam giác SAC
\(\Rightarrow OM||SC\)
\(\Rightarrow OM||\left(SBC\right)\) (2)
Mà OM cắt MN tại M (3)
(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\) (4)
c. Sai
E là trung điểm AB nên OE là đường trung bình tam giác ABD
\(\Rightarrow OE||AD\Rightarrow OE||MN\Rightarrow E\in\left(OMN\right)\)
\(F\in ON\in\left(OMN\right)\Rightarrow EF\in\left(OMN\right)\) (5)
Từ (4);(5) \(\Rightarrow EF||\left(SBC\right)\)
d. Sai
O là tâm đáy nên O cách đều AB và CD
G cách đều AB và CD theo gt
\(\Rightarrow OG||AB||CD\) (6)
Lại có ON là đường trung bình tam giác SBD \(\Rightarrow ON||SB\) (7)
(6);(7) \(\Rightarrow\left(ONG\right)||\left(SAB\right)\)
\(\Rightarrow GN||\left(SAB\right)\)
10.
a. Đúng
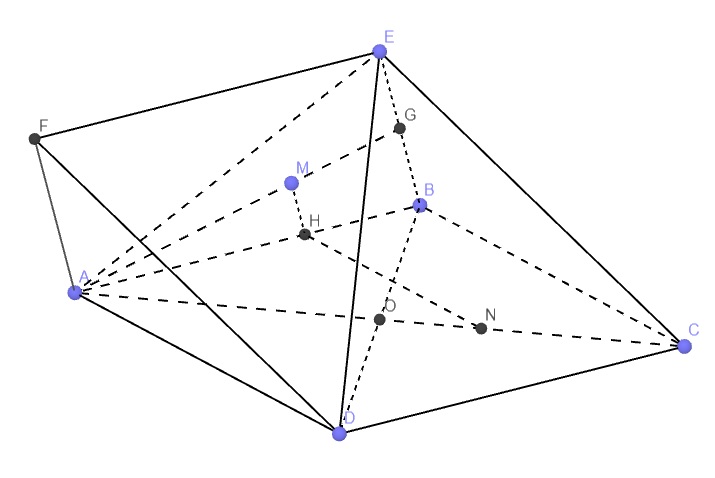
\(\left\{{}\begin{matrix}AB||CD\\AB||EF\end{matrix}\right.\) \(\Rightarrow CD||EF\) (1)
\(\Rightarrow EFDC\) là hình thang
b. Đúng
\(\left\{{}\begin{matrix}AB=CD\\AB=EF\end{matrix}\right.\) (t/c hbh) \(\Rightarrow CD=EF\) (2)
(1);(2) \(\Rightarrow EFDC\) là hình bình hành
\(\Rightarrow FD||EC\) (3)
c. Đúng
Do ABCD là hình bình hành \(\Rightarrow AD||BC\) (4)
Mà AD cắt DF tại D, EC cắt BC tại C (5)
(3);(4);(5) \(\Rightarrow\left(ADF\right)||\left(BCE\right)\)
d. Sai
Gọi G là trung điểm BE, do M là trọng tâm ABE \(\Rightarrow\left\{{}\begin{matrix}M\in AG\\\dfrac{AM}{AG}=\dfrac{2}{3}\end{matrix}\right.\)
Qua M kẻ đường thẳng song song BE cắt AB tại H
\(MH||BE\Rightarrow MH||AF\) \(\Rightarrow MH||\left(ADF\right)\Rightarrow H\in\left(P\right)\)
Qua H kẻ đường thẳng song song AD cắt AC tại N
\(\Rightarrow N\in\left(P\right)\Rightarrow N=AC\cap\left(P\right)\)
Theo định lý Thales: \(\dfrac{AH}{AB}=\dfrac{AM}{AG}=\dfrac{2}{3}\)
\(\dfrac{AN}{AC}=\dfrac{AH}{AB}=\dfrac{2}{3}\)
\(\Rightarrow3AN=2AC=2\left(AN+NC\right)\)
\(\Rightarrow AN=2NC\Rightarrow\dfrac{AN}{NC}=2\)