Ta có:
Tổng khoảng cách từ 1 điểm thuộc Elip đến 2 tiêu điểm bẳng 2a= 5.
Chọn C.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong các phương trình sau, phương trình nào biểu diễn một elíp có khoảng cách giữa các đường chuẩn là 50/3 và tiêu cự 6? A. B. C. D.
Đọc tiếp
Trong các phương trình sau, phương trình nào biểu diễn một elíp có khoảng cách giữa các đường chuẩn là 50/3 và
tiêu cự 6?
A.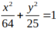 
B. 
C. 
D.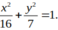 
Trong mặt phẳng với hệ toạ độ Oxy cho elíp
E
:
x
2
9
+
y
2
4
1
và hai điểm A( 3; -2); B( -3;-2) Tìm trên (E) điểm C sao cho tam giác BAC có diện tích lớn nhất. A. C( 0; 3) B.C( 0;2) C. C(3;0) D. C( 1;0)
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho elíp E : x 2 9 + y 2 4 = 1 và hai điểm A( 3; -2); B( -3;-2) Tìm trên (E) điểm C sao cho tam giác BAC có diện tích lớn nhất.
A. C( 0; 3)
B.C( 0;2)
C. C(3;0)
D. C( 1;0)
trong mp oxy, cho điểm a (1;-3). b (0,1): vectơ n= (3;1) a) lập phương trình tổng quát của đường thẳng d đi qua điểm a và có vtpt là n b) lập phương trình thăm số của đường thẳng ab c) tính khoảng cách từ điểm b đến đường thẳng d d) tính góc giữa 2 đường thẳng d và có phương trình 5x-y+1=0
Một (E) có độ dài trục lớn bằng 6, tâm sai bằng \(\dfrac{1}{2}\), khoảng cách từ M thuộc (E) đến tiêu điểm F1 (có hoành độ âm) bằng 7.
a. Tìm khoảng cách từ M đến F2
b. Viết PTCT (E) và tìm M
Cho elip có pt 16x2 + 25y2 = 100. Tính tổng khoảng cách từ điểm thuộc elip đến hai tiêu điểm
Câu 1: Tìm tập hợp các điểm cách đều 2 đường thẳng: Delta3 :3x + 4 y + 6 0 Delta4 :5x -10 0 ( phân giác góc tạo bởi D3 và D4 )Câu 2: Cho hai đường thẳng:Delta : 3x + 2y - 1 0 và d : 5x - 3y+201) Tính khoảng cách từ A(5 ;4) đến đường thẳng Delta2) Viết phương trình các đường phân giác của góc tạo bởi hai đường thẳng trên.3) Tìm điểm M thuộc Delta sao cho khoảng cách từ M đến d bằng 5.4) Tìm điểm N thuộc đường thẳng (D1) : x - 2y 0 bằng hai lần khoảng cách từ N đến d .
Đọc tiếp
Câu 1: Tìm tập hợp các điểm cách đều 2 đường thẳng:
Delta3 :3x + 4 y + 6 = 0
Delta4 :5x -10 = 0 ( phân giác góc tạo bởi D3 và D4 )
Câu 2: Cho hai đường thẳng:
Delta : 3x + 2y - 1 = 0 và d : 5x - 3y+2=0
1) Tính khoảng cách từ A(5 ;4) đến đường thẳng Delta
2) Viết phương trình các đường phân giác của góc tạo bởi hai đường thẳng trên.
3) Tìm điểm M thuộc Delta sao cho khoảng cách từ M đến d bằng 5.
4) Tìm điểm N thuộc đường thẳng (D1) : x - 2y = 0 bằng hai lần khoảng cách từ N đến d .
Cho đường tròn (C):\(x^2+y^2=4\)và điểm A(-2, 3)
a) Viết phương trình của các tiếp tuyến của (C) kể từ A.
b) Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.
Câu 4.(2 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A 1;3 , B 2;1,C0;3 a). Tìm tọa độ trọng tâm tam giác ABC. b). Viết phương trình tổng quát đường trung trực của tam giác ABC. c). Tính khoảng cách từ A đến đường thẳng : x − y + 1 = 0
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2) và B (3; 4). Điểm P ( a b ; 0) (với a b là phân số tối giản, b > 0) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính S = a + b.
A. S = -2
B. S = 8
C. S = 7
D. S = 4