Ta có : ∆ ABF nội tiếp trong (O) và AB là đường kính cuả (O) nên ΔABF vuông tại F
Suy ra: BF ⊥ AK
Mà AK ⊥ CD (gt)
Nên : BF // CD
Suy ra: ∠ BD = ∠ CF
(hai cung bị chắn giữa hai dây song song thì bằng nhau)
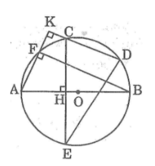
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: Hai cung nhỏ BF và DE bằng nhau
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: DE = BF
Cho đường tròn (O) đường kính AB. Trên cùng nửa đường tròn lấy hai điểm C, D. Kẻ CH vuông góc với AB tại H, CH cắt (O) tại điểm thứ hai E. Kẻ AK vuông góc với CD tại K, AK cắt (O) tại điểm thứ hai F. Chứng minh:
a, Hai cung nhỏ C F ⏜ và D B ⏜ bằng nhau
b, Hai cung nhỏ
B
F
⏜
và
D
E
⏜
bằng nhau
c, DE = BF
Trên nửa đường tròn tâm O, đường kính AB lấy 2 điểm C và D. Kẻ CH vuông góc AB tại H, CH cắt (O) tại E. Kẻ AK vuông góc đường thẳng DC tại K, cắt (O) tại điểm thứ hai là F. Chứng minh :
a)Cung nhỏ CF = cung nhỏ DB
b)Cung nhỏ BF = cung nhỏ DE
c)DE = DF
Giúp mình vs nha !Mình cần gấp lắm !!!
Trên nửa đường tròn tâm O, đường kính AB lấy 2 điểm C và D. Kẻ CH vuông góc AB tại H, CH cắt (O) tại E. Kẻ AK vuông góc đường thẳng DC tại K, cắt (O) tại điểm thứ hai là F. Chứng minh :
a)Cung nhỏ CF = cung nhỏ DB
b)Cung nhỏ BF = cung nhỏ DE
c)DE = DF
giúp mình vs nha !
Trên nửa đường tròn tâm O, đường kính AB lấy 2 điểm C và D. Kẻ CH vuông góc AB tại H, CH cắt (O) tại E. Kẻ AK vuông góc đường thẳng DC tại K, cắt (O) tại điểm thứ hai là F. Chứng minh :
a)Cung nhỏ CF = cung nhỏ DB
b)Cung nhỏ BF = cung nhỏ DE
Giúp mình với mình đang cần gấp
Cho đường tròn (O) đường kính AB. Trên nửa đường tròn lấy 2 điểm C, D. Kẻ CH vuông góc với AB cắt đương tại điểm thứ hai là E. Ke AK vuông goác với CD cắt đường tròn tại điểm thứ 2 la F. CM: DE=BF
Trên (O;\(\frac{AB}{2}\)) lấy 2 điểm C và D tùy ý.Kẻ CH vuông góc AB và cắt đường tròn tại điểm thứ 2 là E. Từ A kẻ AK vuông góc DC cắt đường tròn tại điểm thứ hai là F
a) CM: cung CF nhỏ = DB nhỏ.
b) CM: cung BF nhỏ = DE nhỏ
Trên nửa đường tròn tâm O đường kính AB với AB = 2022, lấy điểm C (C khác A và B), từ C kẻ CH vuông góc với AB (H thuộc AB). Gọi D là điểm bất kỳ trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E. a) Chứng minh tứ giác BHDE là tứ giác nội tiếp; b) Chứng minh: AD.EC=CD.AC; c) Chứng minh: AD.AE+BH.BA=2022^2
