Các câu hỏi tương tự
cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2 TC.TD . 4 điểm o, d,c,e cùng nằm trên đường tròn
Đọc tiếp
cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2= TC.TD . 4 điểm o, d,c,e cùng nằm trên đường tròn
Cho đường tròn tâm (O;R) dây AB cố định ( AB < 2R) và C là một điểm di động trên cung lớn AB gọi N là điểm chính giữa cung nhỏ ab m là điểm chính giữa cung ac không chứa điểm b h là giao điểm của nm và ac không chứa điểm b, h là giao điểm của mn và ac k là giao điểm bm và cn
Xác định vị trí của điểm C thỏa mãn tứ giác AKBN có diện tích lớn nhất
Cho đường tròn (O) đường kính AB
4
3
cm. Điểm
C
∈
(
O
)
sao cho
A
B
C
^
30
°
. Tính diện tích hình viên phân AC . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy ) A.
π
-
3
3
cm...
Đọc tiếp
Cho đường tròn (O) đường kính AB = 4 3 cm. Điểm C ∈ ( O ) sao cho A B C ^ = 30 ° . Tính diện tích hình viên phân AC . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy )
A. π - 3 3 cm 2
B. 2 π - 3 3 cm 2
C. 4 π - 3 3 cm 2
D. 2 π - 3 cm 2
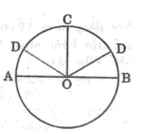
Cho đường tròn (O;R), đường kính AB .Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm BOD. Có mấy đáp số
Cho đường tròn tâm O và 1 điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp điểm MA, MB với đường tròn, Gọi C là 1 điểm trên cung AB của đường tròn tâm M bán kính MA, (cung AB nằm trong dường tròn (O)). Các tia AC,BC cắt dường tròn (O) tại P và Q. Chứng minh rằng PQ đi qua O
Cho đường tròn (O; R), đường kính AB. Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm DOB. Có mấy đáp số ?
Cho nửa đường tròn (O) có đường kính AB 2R ( R 0). Gọi C là điểm chính giữa của cung AB và M là điểm thuộc cung BC ( O khác B và C). Tiếp tuyến tại M của nửa đtròn (O) cắt các đường thẳng OC và AB theo thứ tự tại S và K. AN cắt OC tại Ia) Tính diện tích hình viên phân giới hạn bởi dây AC và cung AC ( tính theo R)b) CM tứ giác OIMB là tứ giác nội tiếp và SI SMc) CM AC là tiếp tuyến của đtròn ngoại tiếp tam giác ICMd) Gọi H là hình chiếu của M trên AB. CM BH.AK BK.AH
Đọc tiếp
Cho nửa đường tròn (O) có đường kính AB= 2R ( R> 0). Gọi C là điểm chính giữa của cung AB và M là điểm thuộc cung BC ( O khác B và C). Tiếp tuyến tại M của nửa đtròn (O) cắt các đường thẳng OC và AB theo thứ tự tại S và K. AN cắt OC tại I
a) Tính diện tích hình viên phân giới hạn bởi dây AC và cung AC ( tính theo R)
b) CM tứ giác OIMB là tứ giác nội tiếp và SI= SM
c) CM AC là tiếp tuyến của đtròn ngoại tiếp tam giác ICM
d) Gọi H là hình chiếu của M trên AB. CM BH.AK= BK.AH
Cho đường tròn tâm O và 1 điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp điểm MA, MB với đường tròn, Gọi C là 1 điểm trên cung AB của đường tròn tâm M bán kính MA, (cung AB nằm trong dường tròn (O)). Các tia AC,BC cắt dường tròn (O) tại P và Q. Chứng minh rằng PQ đi qua O
Cho đường tròn tâm O, bán kính R=3 cm và hai điểm A,B nằm trên đường tròn (O) sao cho số đo cung lớn bằng 240°. Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB vsf cung nhỏ AB.









