a, HS tự chứng minh
b, Ta chứng minh được tứ giác BCEN là hình bình hành => BC = EN
Do BCDE là hình bình hành
=> BC = ED; DE = EN
=> BA ⊥ EN => BABC
=> BC là tiếp tuyến
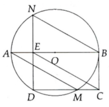
Cho đường tròn tâm O , đường kính AB . Dây AM và BN song song với nhau sao cho sđ cung BM < 900900 . Vẽ dây MD // AB , dây DN cắt AB tại E . Từ E vẽ một đường thẳng song song với AM cắt đường thẳng DM tại C . Chứng minh:
a. AB ⊥ DN
b. BC là tiếp tuyến đường tròn (O)
Cho đường tròn (O) đường kính AB. Vẽ 2 dây AM và BN song song sao cho sđ cung BM<90 độ. Vẽ dây MD song song với AB. Dây DN cắt AB tại F. Từ R vẽ 1 đường thẳng song song với AM cắt DM tại C. Chứng minh:
a, AB vuông góc DN
b, BC là tiếp tuyến của (O)
Cho (O) đường kính AB. Vẽ hai dây AM và BN song song với nhau sao cho Sđ cung BM<90°. Vẽ dây MD song song với AB. Dây DN cắt AB tại E. Từ E vẽ 1 đường thẳng // với AM cắt DM tại C. CMR:
a) AB vuông góc DN.
b) BC là tiếp tuyến (O).
cho đường tròn (O) đường kính AB.Vẽ hai dây AM và BN song song với nhau sao cho số đo cung BM<90 độ .Vẽ dây MD//AB.Dây DN cắt AB tại E.Từ E vẽ một đường thẳng song song với AM cắt đường thẳng DM tại C.Chứng minh rằng:
a.AB vuông góc DN
b.BC là tiếp tuyến của (O)
Cho đường tròn (O) , đường kính AB .Vẽ 2 dây AM và BM song song với nhau sao cho sđ cung BM < 90. . Vẽ dây MD song song với AB . Dây AN cắt AB tại E . Đường thẳng qua E song song với AM cắt DM tại C . Chứng minh rằng
a) Cung AD = cung AN và AB \(\perp\)DN
b) BC là tiếp tuyến của (O)
Cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn (O;R). Vẽ đường kính AD, tiếp tuyến với đường tròn (O;R) tại D cắt BC tại E. Vẽ OH vuông góc với BC
a/ Chứng minh tứ giác OHDE nội tiếp
b/ Chứng minh ED^2=EC.EB
c/ Từ C vẽ đường thẳng song song với EO cắt AD tại I. Chứng minh HI song song với AB
d/ Qua D vẽ đường thẳng song song với EO cắt AB và AC lần lượt tại M và N. Chứng minh DM=DN
Cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn (O;R). Vẽ đường kính AD, tiếp tuyến với đường tròn (O;R) tại D cắt BC tại E. Vẽ OH vuông góc với BC
a/ Chứng minh tứ giác OHDE nội tiếp
b/ Chứng minh ED^2=EC.EB
c/ Từ C vẽ đường thẳng song song với EO cắt AD tại I. Chứng minh HI song song với AB
d/ Qua D vẽ đường thẳng song song với EO cắt AB và AC lần lượt tại M nà N. Chứng minh DM=DN
Cho đường tròn (O;R) dây AB khác đường kính. Qua O vẽ đường thẳng vuông góc với AB tại H, cắt tiếp tuyến tại A của đường tròn ở O
a) CM: CB là tiếp tuyến của đường tròn (O)
b) kẻ đường thẳng qua A song song với CO cắt đường tròn (O) tại D. Vẽ AK vuông góc với BD. CM: 3 điểm BOD thẳng hàng và tam giác AKD đồng dạn với tam giác CAO
c) Đường thẳng CO cắt (O) tại hai điểm M và N, (M nằm giữa C và N). CM: MC.NH=MH.NC
