Các câu hỏi tương tự
Cho đường tròn (O;R) và đường thẳng d cố định, sao cho khoảng cách từ tâm O đến đường thẳng d lớn hơn bán kìn R của đường tròn O. Trên đường thẳng d lấy điểm M bất kỳ. Từ M kẻ MC là tiếp tuyến của đường tròn (O;R), C là tiếp điểm. Vẽ CH vuông góc với OM tại H, cắt (O;R) tại B.a) Cho biết vị trí tương đối của đường tròn (O;R) và đường thẳng d? Giải thích vì sao?b) Chứng minh: MB là tiếp tuyến của (O;R)c) Chứng minh rằng: Khi điểm M di chuyển trên đường thẳng d thì đoạn thẳng BC luôn đi qua 1 điể...
Đọc tiếp
Cho đường tròn (O;R) và đường thẳng d cố định, sao cho khoảng cách từ tâm O đến đường thẳng d lớn hơn bán kìn R của đường tròn O. Trên đường thẳng d lấy điểm M bất kỳ. Từ M kẻ MC là tiếp tuyến của đường tròn (O;R), C là tiếp điểm. Vẽ CH vuông góc với OM tại H, cắt (O;R) tại B.
a) Cho biết vị trí tương đối của đường tròn (O;R) và đường thẳng d? Giải thích vì sao?
b) Chứng minh: MB là tiếp tuyến của (O;R)
c) Chứng minh rằng: Khi điểm M di chuyển trên đường thẳng d thì đoạn thẳng BC luôn đi qua 1 điểm cố định.
Từ điểm S nằm ngoài đường tròn tâm (O;R) vẽ hai tiếp tuyến SA;SB (A;B là các tiếp điểm ). Cát tuyến SMN cắt bán kính OB. Gọi Q là trung điểm MN .a)Chứng minh tứ giác SAOQ nội tiếp đường tròn .b)Chứng minh QS là phân giác của góc AQB . c)Qua Q vẽ đường thẳng vuông góc với OS cắt tia SA,SB thứ tự tại C,D. Khi (O;R) và đường thẳng MN cố định .Tìm vị trí của S trên đường thẳng MN để diện tích tam giác SCD nhỏ nhất
Đọc tiếp
Từ điểm S nằm ngoài đường tròn tâm (O;R) vẽ hai tiếp tuyến SA;SB (A;B là các tiếp điểm ). Cát tuyến SMN cắt bán kính OB. Gọi Q là trung điểm MN .
a)Chứng minh tứ giác SAOQ nội tiếp đường tròn .
b)Chứng minh QS là phân giác của góc AQB .
c)Qua Q vẽ đường thẳng vuông góc với OS cắt tia SA,SB thứ tự tại C,D. Khi (O;R) và đường thẳng MN cố định .Tìm vị trí của S trên đường thẳng MN để diện tích tam giác SCD nhỏ nhất
Cho đường tròn tâm O bán kính R điểm A nằm ngoài đường trong tâm O sao cho AO=2R. từ A vẽ 2 tiếp tuyến AB,AC với đường tròn (BC là các tiếp điểm) đoạn thẳng OA cắt đường tròn tâm O tại I đường thẳng qua O và vuông góc với OB cắt AC tại K.Chứng minh rằng: a, Tam giác OAK cân tại A b,KI là tiếp tuyến của đường tròn tâm O
Cho Đường Tròn Tâm (O) Đường Kính BC . Điểm A Chuyển Động Trên Đường Tròn (O) ;(A Khác B Và C ) . Gọi H Là Hình Chiếu Của A Trên BC . Vẽ Đường Tròn Tâm A , Bán Kính AH Cắt Đường Tròn (O) Tại D Và E .
Chứng Minh :
a) Đường Thẳng DE Đi Qua Trung Điểm K Của AH.
b) Xác Định Vị Trí Của Điểm A Để DE Có Độ Dài Lớn Nhất , Tính Độ Dài Lớn Nhất Đó Theo R.
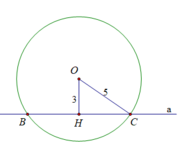
Cho đường thẳng a và có một điểm O cách a là 3cm. Vẽ đường tròn tâm O bán kính 5cm.a) Đường thẳng a có vị trí như thế nào đối với đường tròn (O) ? Vì sao ?b) Gọi B và C là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài BC.
Đọc tiếp
Cho đường thẳng a và có một điểm O cách a là 3cm. Vẽ đường tròn tâm O bán kính 5cm.
a) Đường thẳng a có vị trí như thế nào đối với đường tròn (O) ? Vì sao ?
b) Gọi B và C là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài BC.
Cho đường tròn tâm O bán kính R lấy 2 điểm A và B của đường tròn sao cho cắt AB=R. Qua A vẽ đường thẳng vông góc vs OA tại A cắt đường trung trực của AB tại O' bán kính O'A, vẽ C đối xứng vs AB qua O và D đối xứng vs A qua O' .
a, B\(\in\) đường tròn tâm O' bán kính O'A.b, Chứng minh B,C,D thẳng hàng.c, tính bán kính đường tròn tâm O' và CD theo R.Cho đường tròn (O;R) và cắt tuyến d bất kì không đi qua O.Lấy 1 điểm M thuộc d và nằm bên ngoài đường tròn. Đường M vẽ hai tiếp tuyến MA và MB tới đường tròn ( A,B là các tiếp tuyến).Kẻ đường kính AOC.a)C/m BC//OMb)Qua O vẽ đường thẳng vuông góc vs AC,cắt đường thẳng BC tại D.C/m MDRc)Các tứ giác OAMD,ODBM là hình gì?d) C/m 5 điểm O,A,B,D,M cùng thuộc 1 đường tròn.Xác định tâm I của đường tròn đó.e) Gọi K là giao điểm của OD và BMH là giao điểm của OB và MD.C/m rằng 3 điểm H,I,K thẳng hàng.f)Xác...
Đọc tiếp
Cho đường tròn (O;R) và cắt tuyến d bất kì không đi qua O.Lấy 1 điểm M thuộc d và nằm bên ngoài đường tròn. Đường M vẽ hai tiếp tuyến MA và MB tới đường tròn ( A,B là các tiếp tuyến).Kẻ đường kính AOC.
a)C/m BC//OM
b)Qua O vẽ đường thẳng vuông góc vs AC,cắt đường thẳng BC tại D.C/m MD=R
c)Các tứ giác OAMD,ODBM là hình gì?
d) C/m 5 điểm O,A,B,D,M cùng thuộc 1 đường tròn.Xác định tâm I của đường tròn đó.
e) Gọi K là giao điểm của OD và BMH là giao điểm của OB và MD.C/m rằng 3 điểm H,I,K thẳng hàng.
f)Xác định vị trí của điểm M trên d để tam giác EAM là tam giác đều.
cho đường tròn (O;R) ( điểm O cố định giá trị R k đổi ) và điểm M nằm ngoài (O). kẻ 2 tiếp tuyến MB,MC(B,C là các tiếp điểm) và tia Mx nằm giữa hai tia MB và MC. qua B kẻ đường thẳng song song với Mx, đường thẳng này cắt (O) tại điểm thứ 2 là A. Vẽ đường kính BB của (O). qua O kẻ đường thẳng vuông góc với BB , đường thẳng này cắt MB và BC lần lượt tại K và E.cmra) 4 điểm M,B,O,C nằm trên một đường trònB) MERc) khi M di động mà OM 2R thì điểm K di động trên một đường tròn cố định , chỉ rõ tâm và...
Đọc tiếp
cho đường tròn (O;R) ( điểm O cố định giá trị R k đổi ) và điểm M nằm ngoài (O). kẻ 2 tiếp tuyến MB,MC(B,C là các tiếp điểm) và tia Mx nằm giữa hai tia MB và MC. qua B kẻ đường thẳng song song với Mx, đường thẳng này cắt (O) tại điểm thứ 2 là A. Vẽ đường kính BB' của (O). qua O kẻ đường thẳng vuông góc với BB' , đường thẳng này cắt MB và B'C lần lượt tại K và E.cmr
a) 4 điểm M,B,O,C nằm trên một đường tròn
B) ME=R
c) khi M di động mà OM= 2R thì điểm K di động trên một đường tròn cố định , chỉ rõ tâm và bán kính đường tròn đó
Cho đường thẳng a và có một điểm O cách a là 3cm. Vẽ đường tròn tâm O bán kính 5cm.
Đường thẳng a có vị trí như thế nào đối với đường tròn (O) ? Vì sao ?
Cho đường tròn tâm O và đường thẳng d không giao nhau với đường tròn. Trên d lấy M bất kì, qua M kẻ 2 tiếp tuyến MA, MB(A,B là các tiếp điểm). Gọi H là hình chiếu của O lên d, AB cắt OH và OM lần lượt ở I và K.a, Chứng minh: r^2OI.OHOK.OM ( r là bán kính đường tròn tâm O)b, Chứng minh khi M di chuyển trên đường thẳng d thì đường tròn ngoại tiếp tam giác MIK luôn đi qua 2 điểm cố định
Đọc tiếp
Cho đường tròn tâm O và đường thẳng d không giao nhau với đường tròn. Trên d lấy M bất kì, qua M kẻ 2 tiếp tuyến MA, MB(A,B là các tiếp điểm). Gọi H là hình chiếu của O lên d, AB cắt OH và OM lần lượt ở I và K.
a, Chứng minh: r^2=OI.OH=OK.OM ( r là bán kính đường tròn tâm O)
b, Chứng minh khi M di chuyển trên đường thẳng d thì đường tròn ngoại tiếp tam giác MIK luôn đi qua 2 điểm cố định










