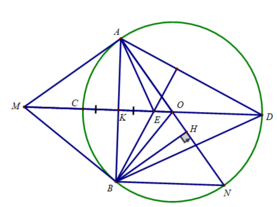
c) Ta có: ∠(ABN ) = 90 0 (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90 0
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
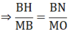
Hay MB. BN = BH. MO
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
b) Tính MA, AB, OK theo R.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
Cho đường tròn (O; R). Điểm M ở bên ngoài đường tròn sao cho OM= 2R. Kẻ hai tiếp tuyến MA, MB tời đường tròn (A;B là các tiếp điểm). Nối OM cắt AB tại H. Hạ HD vuông góc MA tại D. Điểm C thuộc cung nhỏ AB. Tiếp tuyến tại C của đường tròn (O;R) cắt MA, MB lần lượt tại E và F. Đường tròn đường kính BM cắt BD tại I. Gọi K là trung điểm của OA. Chứng minh ba điểm M, I, K thẳng hàng
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
b) Tính MA, AB, OK theo R.
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Cho đường tròn (O;R). Điểm M ở ngoài đường tròn sao cho OM = 2R. Kẻ hai tiếp tuyến MA, MB tới đường tròn (A, B là các tiếp điểm). Nối OM cắt AB tại H. Hạ HD ⊥ MA tại D. Đường tròn đường kính MB cắt BD tại I. K là trung điểm AO. Chứng minh: M,I,K thẳng hàng.
Cho đường tròn ( O). Điểm M nằm ngoài đường tròn. Kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm)
a, Chứng minh OM vuông góc với AB
b, Gọi H là giao điểm của MO và AB. Kẻ đường thẳng MO cắt đường tròn ( O) lần lượt tại hai điểm P, Q ( P nằm giữa M và O). Chứng minh QH.AM=QM.AH
Cho đường tròn(O; R), điểm M nằm phía bên ngoài đường tròn sao cho OM = 2R. Từ điểm M kẻ các tiếp tuyến MB, MC với đường tròn (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OM và BC. a) Chứng minh: OM ⊥ BC tại H. b) Kẻ đường kính BD, chứng minh: CD//OM c) Tính MH.MO theo R. Tính 𝐵𝑀𝐶 = ? d) MD cắt đường tròn (O) tại điểm thứ hai là E. Chứng minh: MH.MO = ME.MD
Cho đường tròn (O,R) cố định.Từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB (A,B là các tiếp điểm).Gọi H là giao điểm của OM,AB
a) CM: OM vuông góc với AB và OH.OM=R2
b) Từ M kẻ cát tuyến MNP với đường tròn (O) (N nằm giữa M,P),gọi I là trung điểm NP (I khác O).Chứng minh: A,M,O,I thuộc một đường tròn và tìm tâm của đường tròn đó
c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA,MB theo thứ tự C,D.Biết MA=5cm ,tính chu vi tam giác MCD
d) Qua O kẻ đường thẳng d vuông góc với OM, cắt MA,MB lần lượt tại E,F.Xác định vị trí của điểm M để diện tích tam giác MEF nhỏ nhất
~Giải nhanh giùm mình nhé~
