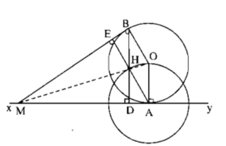
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.

Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Khi M di chuyển trên xy thì H di chuyển trên đường nào ?
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Tứ giác AOBH là hình gì?
Cho đường tròn ( O; R ) , điểm A cố định nằm trên đường tròn , kẻ tiếp tuyến d qua A với ( O ) . Trên d lấy điểm M ( M khác A ) , từ M kẻ tiếp tuyến thứ 2 là MB với ( O ) ( B là tiếp điểm )
a, CM 4 điểm A , O , B , M cùng nằm trên 1 đt
b , Đoạn OM cắt đtròn ( O ) tại I . Chứng minh BI là phân giác của góc MAB . Từ đó suy ra I là tâm của đtròn nội tiếp tam giác MAB
c, gọi H là trực tâm của tam giác MAB . Điểm H chạy trên đường nào khi M chạy trên d
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Cho đường tròn (O;R). Từ điểm A nằm bên ngoài đường tròn kẻ các tiếp tuyến AC, AC với đường tròn (B và C là các tiếp điểm). Gọi H là trung điểm của BC
a. Chứng minh 3 điểm A,B,C,O thuộc 1 đường tròn
b. Chứng minh 3 điểm A,H,O thẳng hàng.Kẻ đường kính BD của đường tròn (O;R). Vẽ CK vuông góc với BD. Chứng minh \(AC.CD=CK.AO\)
c. Gọi giao điểm của AO với đường tròn tâm O là N. Chứng minh N là tâm đường tròn nội tiếp tam giác ABC
d.Khi A di động trên tia By cố định, gọi M là trực tâm của tam giác ABC. Chứng minh M di động trên 1 đường cố định
Cho ba điểm A,B,C cố định, thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi nhưng luôn đi qua hai điểm C và B ( O không thuộc BC). Từ A vẽ hai tiếp tuyến AM và AN với đường tròn (O) ( M. N là hai tiếp điểm). Gọi I là trung điểm của BC.
1) Chứng minh bốn điểm O, I, A, M cùng thuộc một đường tròn.
2) Gọi E, H lần lượt là giao điểm của OA với đường tròn (O) và MN. Chứng minh BE là tia phân giác của góc ABH.
3) Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác OHI luôn nằm trên một đường thẳng cố định
Cho đường tròn (O) điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF).Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO)
a, Chứng minh MA. MB = ME.MF
b, Gọi H là hình chiêu vuông góc của điểm c lên đuờng thẳng MO. Chứng minh tứ giác AHOB nội tiếp
c, Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh các đường thẳng MS và KC vuông góc nhau
d, Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng
Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME<MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).
a. Chứng minh rằng MA.MB = ME.MF
b. Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.
c. Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.
d. Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng.
Cho đường tròn (O) và đường thẳng xy không có điểm chung với đường tron f(O). Gọi A là hình chiếu của O trên đường thẳng xy. Qua A vẽ cát tuyến không đi qua O cắt đường tròn tại hai điểm B và C (AB < AC). Tiếp tuyến của đường tròn tại hai điểm B và C cắt đường thẳng xy lần lượt taiij M và N.
a) Chứng minh tứ giác ABOM nội tiếp.
b) Chứng minh góc BCO bằng góc ANO và tam giác OMN cân.
c) Giả sử đường tròn (O) và đường thẳng xy cố định. Từ M vẽ tiếp tuyến thứ hai ME với đường tròn (O), E là tiếp điểm khác B. Chứng minh khi cát tuyến ABC di chuyển quanh A thì BE luôn đi qua một điểm cố định.
GIÚP MÌNH CÂU C VỚI!!!