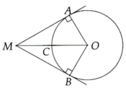
a, Sử dụng tỉ số lượng giác trong tam giác vuông ∆AMO ta tính được A O M ^ = 60 0
b, Tính được A O B ^ = 120 0 , sđ A B C ⏜ = 120 0
c, Ta có A O C ⏜ = B O C ⏜ => A C ⏜ = B C ⏜

a, Sử dụng tỉ số lượng giác trong tam giác vuông ∆AMO ta tính được A O M ^ = 60 0
b, Tính được A O B ^ = 120 0 , sđ A B C ⏜ = 120 0
c, Ta có A O C ⏜ = B O C ⏜ => A C ⏜ = B C ⏜
Bài 7: Cho đường tròn (O; R), điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA,
MB với đường tròn (A, B là các tiếp điểm). Nối MO cắt cung nhỏ AB tại N
a) Cho OM = 2R. Tính AON và số đo A NB
b) Biết AMB = 36o . Tính góc ở tâm hợp bởi hai bán kính OA, OB.
Bài 8: Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O)
cắt AB, AC tương ứng tại M và N.
a) Chứng minh các cung nhỏ BM và CN có số đo bằng nhau
b) Tính MON , nếu BAC =40o
Bài 9: Trên cung nhỏ AB của đường tròn (O), cho hai điểm C, D sao cho cung AB được
chia thành ba cung bằng nhau, tức là AC =CD =DB . Bán kính OC và OD cắt dây AB lần
lượt tại E và F.
a) Hãy so sánh các đoạn thẳng AE, EF và FB
b) Chứng minh rằng AB // CD
Cả hình giúp mình nhé! mơn trc nà![]()
Cho đường tròn (O; R). Điểm M ở bên ngoài đường tròn sao cho OM= 2R. Kẻ hai tiếp tuyến MA, MB tời đường tròn (A;B là các tiếp điểm). Nối OM cắt AB tại H. Hạ HD vuông góc MA tại D. Điểm C thuộc cung nhỏ AB. Tiếp tuyến tại C của đường tròn (O;R) cắt MA, MB lần lượt tại E và F. Đường tròn đường kính BM cắt BD tại I. Gọi K là trung điểm của OA. Chứng minh ba điểm M, I, K thẳng hàng
Bài 1:
Cho (O;R), và một điểm M nằm ngoài đường tròn (O) sao cho OM = 2R. Từ M vẽ tiếp
tuyến MA của đường tròn (O) (A là tiếp điểm)
a) Tính độ dài AM theo R
b) Từ A kẻ dây cung AB vuông góc với OM tại H. Chứng minh MB là tiếp tuyến của
đường tròn (O)
(vẽ hình)
Từ điểm M nằm ngoài đường tròn (O;R) kẻ các tiếp tuyến MA,MB của đường
tròn (O) (A và B là các tiếp điểm, OM > 2R). Gọi E là trung điểm của đoạn thẳng MB,
C là giao điểm của đường thẳng AE với đường tròn (O) và tia MC cắt đường tròn (O)
tại điểm thứ hai D.
a) Chứng minh: tử giác MAOB nội tiếp và gócMOB = gócADB;
b) Chứng minh: BF^2 = EC EA và AD ||MB.
c) Kẻ đường kính BI của đường tròn (O). Đường thẳng MI và đường thẳng AD
cắt nhau tại K . Chứng minh: KD = 3KA.
Cho đường tròn(O; R), điểm M nằm phía bên ngoài đường tròn sao cho OM = 2R. Từ điểm M kẻ các tiếp tuyến MB, MC với đường tròn (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OM và BC. a) Chứng minh: OM ⊥ BC tại H. b) Kẻ đường kính BD, chứng minh: CD//OM c) Tính MH.MO theo R. Tính 𝐵𝑀𝐶 = ? d) MD cắt đường tròn (O) tại điểm thứ hai là E. Chứng minh: MH.MO = ME.MD
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Câu 4:( 4 điểm ) Từ điểm M nằm ngoài đường tròn ( O,R ) sao cho OM = 3R, vẽ các tiếp tuyến MA, MB với đường tròn ( O,R ) (A, B là các tiếp điểm). a ) Chứng minh: Tứ giác MAOB nội tiếp và OM là đường trung trực của đoạn AB. b ) Tính độ dài đoạn thẳng MA, AB theo R. c) Vẽ dây AC song song MB, đường thẳng MC cắt đường tròn (O,R) tại điểm thứ hai là D, tia AD cắt MB tại E. Chứng minh: E là trung điểm của đoạn MB
cho đường tròn ( O,R). M LÀ MỘT ĐIỂM SAO CHO OM=2R. TỪ M KẺ HAI TIẾP TUYẾN MA, MB VỚI(O) ( TRONG ĐÓ A.B LÀ CÁC TIẾP ĐIỂM, A KHÁC B)
a) TÍNH MA THEO R
b) CHỨNG MINH TAM GIÁC ABM LÀ TAM GIÁC ĐỀU
c) GỌI N LÀ ĐIỂM THUỘC CUNG NHỎ AB. QUA N KẺ TIẾP TUYẾN VỚI (O), NÓ CẮT CÁC TIẾP TUYẾN Ax, By THEO THỨ TỰ TẠI C VÀ D. TÍNH TỈ SỐ CHU VI CỦA HAI TAM GIÁC MCD VÀ MAB
Cho đường tròn tâm O bán kính R. Từ điểm M là điểm ngoài đường tròn kẻ hai tia tiếp tuyến MA; MB (A,B là tiếp điểm) và cát tuyến đi qua M cắt đường tròn tại C, D (C nằm giữa M và D) cung CAD nhỏ hơn cung CBD. Gọi E là giao điểm của AB với OM.
a. Chứng minh DEC = 2.DBC.
b. Từ O kẻ tia Ot vuông góc với CD cắt tia BA ở K. Chứng minh KC và KD là tiếp tuyến của đường tròn O.