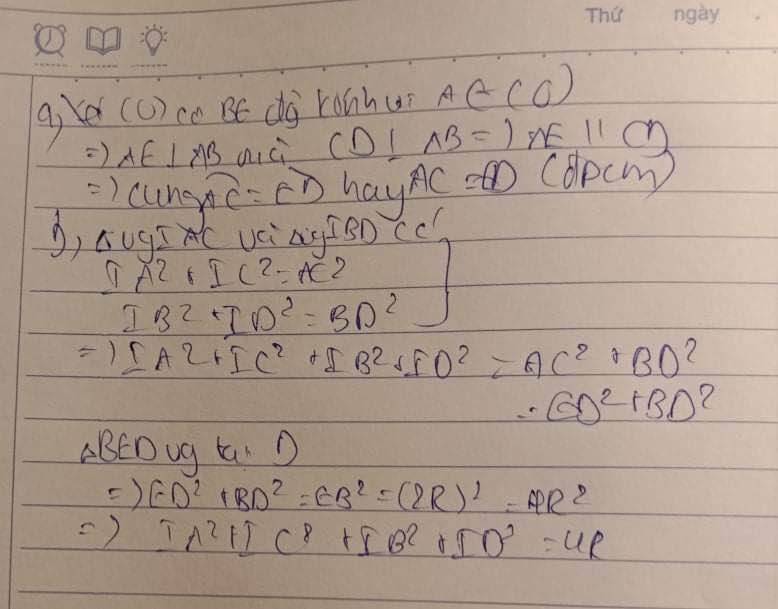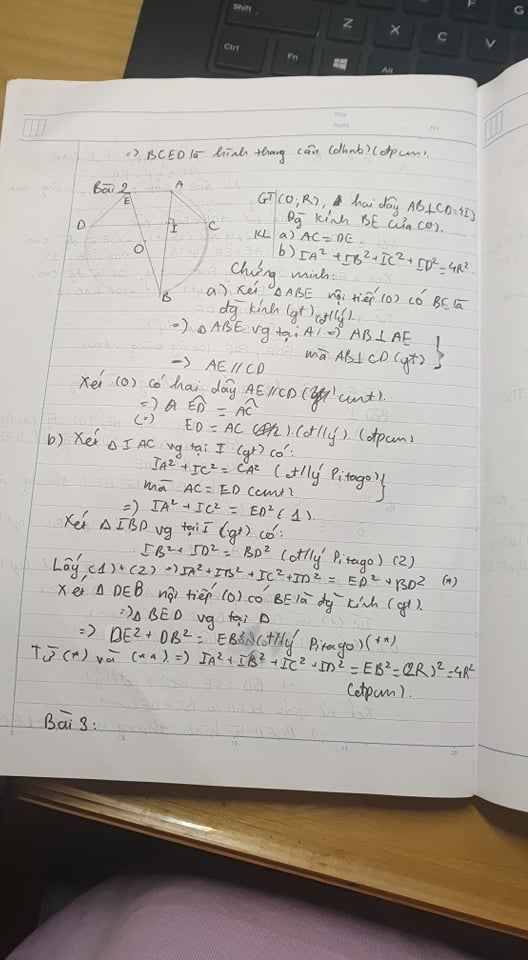Question

Cho đường tròn (O ; R) hai dây cung AB và CD vuông góc với nhau tại I (C thuộc cung nhỏ AB). Kẻ đường kính BE của đường tròn (O). Chứng minh:

a) $AC = DE.$

b) $IA^2+IB^2+IC^2+ID^2=4R^2.$

Answer 1

a) ^EAB là góc nội tiếp chắn nửa đường tròn nên ^EAB = 90⁰ hay AE⊥AB

Có AE⊥AB (cmt) và CD⊥AB (gt) nên AE//CD => Cung AC bằng cung DE hay AC = DE (đpcm)

b) ∆AIC và ∆BID vuông tại I nên IA² + IB² + IC² + ID² = (IA² + IC²) + (IB² + ID²) = AC² + BD² = ED² + BD² = BE² (∆EDB có ^EDB = 90⁰ do nó là góc nội tiếp chắn nửa đường tròn)

Mà BE² = (2R)² = 4R² nên IA² + IB² + IC² + ID² = 4R² (đpcm)

Answer 2

a) ^EAB là góc nội tiếp chắn nửa đường tròn nên ^EAB = 90⁰ hay AE⊥AB

Có AE⊥AB (cmt) và CD⊥AB (gt) nên AE//CD => Cung AC bằng cung DE hay AC = DE (đpcm)

b) ∆AIC và ∆BID vuông tại I nên IA² + IB² + IC² + ID² = (IA² + IC²) + (IB² + ID²) = AC² + BD² = ED² + BD² = BE² (∆EDB có ^EDB = 90⁰ do nó là góc nội tiếp chắn nửa đường tròn)

Mà BE² = (2R)² = 4R² nên IA² + IB² + IC² + ID² = 4R² (đpcm)

 

Answer 3

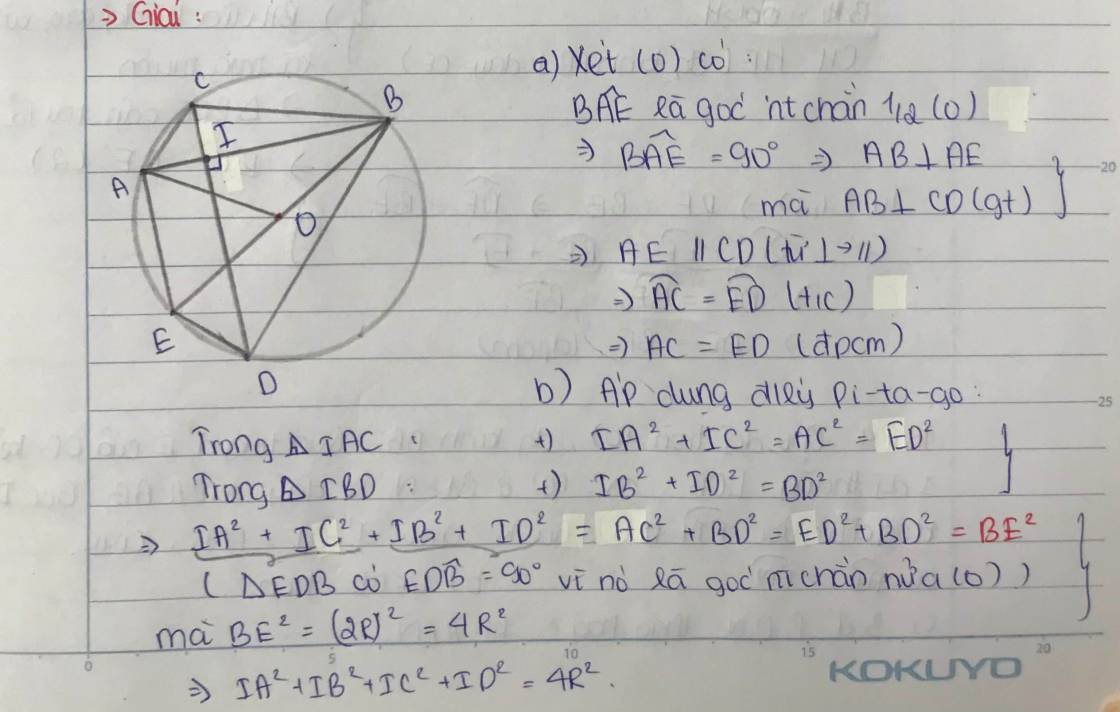
a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O)

⇒ góc BAE = 90 độ.

⇒ AE vuông góc với AB tại A

Mà CD vuông góc với AB tại I (GT)

⇒AE// CD ( định lí từ vuông góc đến song song)

- Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD.

⇒ cung AC = cung ED

⇒ AC = ED ( theo định lí giữa cung và dây cung )

b) CM được góc BDE = 90 độ

⇒ ED^2 + DB^2 = BE^2

⇒ AC^2 + ( IB^2 + ID^2 ) = ( 2R )^2 . ( vì ED = AC, định lí Pytago cho△BID vuông tại I )

⇒( IA^2 + IC^2 ) + ( IB^2 + ID^2 ) = 4R^2. ( định lí Pytago cho△ AIC vuông tại I )

 ⇒ Đcpcm

 

Answer 4

a,

Đường tròn tâm O có góc AEB là góc nộp tiếp chắn nữa đường tròn

nên góc AEB =90 độ nên AB vuông góc với AE,màAB vuông góc với CD 

Suy ra AE song song với CD 

đường tròn tâm O có AE song somg với CD 

nên cung AC bằng cung ED

suy ra AC=ED

b,

có AB vuông góc với CD tại I 

Nên tam giác AIC vuông tại I

nên AI² +IC²=AC²

CHỨNG minh tương tự có ID²+IB²=BD²

Suy ra IA²+ IB²+IC²+ID²=AC²+BD² =DE²+BD²,mà tam giác BED vuông tại D( góc nội tiếp chắn nửa đường tròn)nên DE²+BD²=BE²

SUY RA IA²+IB²+IC²+ID²=BE²=(2 R)²=4R²

Answer 5

ta CM được CD//AE ( cùng vuông góc CD) 

=> cung AC=cung DE ( tính chất)

Áp dụng định lí Pi-ta-go ta có 

IA^2+IC^2=AC^2=DE^2

IB^2+ID^2=BD^2 

từ 2 điều trên suy ra IA2+IB^2+IC^2+ID^2=DE^2+BD^2 = EB^2=(2R)^2=4R^2

IA^2+IC^2=AC^2=DE^2

 

 

                

 

Answer 6

Answer 7

a, Góc BAE=90 độ ( góc nt chắn nửa đường tròn)

=>AB vuông góc với AE tại A hay AI vuông góc với AE ( I thuộc AB) (1)

BI vuông góc với CD (2)

Từ (1) và (2) => AE//CD 

=> cung AC = cung ED ( định lý)

=> AC = DE

b, AI vuông góc với CD tại I ( AB vuông góc CD)

=> Tam giác AIC vuông tại I

AI\(^2\)+ IC\(^2\)=AC\(^2\)

CMTT => ID\(^2\)+IB\(^2\)=BD\(^2\)

=> \(IA^2\)+\(IB^2\)+\(IC^2\)+\(ID^2\)=\(AC^2\)+\(BD^2\)=\(DE^2\)+\(BD^2\)

Mà tam giác BED vuông tại D (góc nt chắn nửa đường tròn) =>\(DE^2+BD^2=BE^2\)=>\(IA^2+IB^2+IC^2+ID^2=BE^2=\left(2R\right)^2=4R^2\)

 

Answer 8

a) Ta có: \(\Delta\)ABE nội tiếp đường tròn (O), đường kính BE

=> \(\Delta ABE\) vuông tại A

=> \(AB\perp AE\)

mà \(AB\perp CD\) (GT)

=> AE // CD

Xét đường tròn (O) có: AE // CD (cmt)

=> cung AC = cung DE ( 2 cung nằm giữa 2 dây song song thì bằng nhau )

=> AC = DE ( liên hệ giữa cung và dây )  (đpcm)

b) \(\Delta AIC\) có:  {\displaystyle \angle } AIC = 90° ( do \(AB\perp CD\) )

=> IC² + IA² = AC² ( Py-ta-go )

mà AC = DE ( câu a )

=> IC² + IA² = DE²     (1)

\(\Delta BID\) có:  {\displaystyle \angle } BID = 90° ( do \(AB\perp CD\))

=> IB² + ID² = BD²          (2)

Ta có:  \(\Delta BDE\) nội tiếp đường tròn (O), đường kính BE

=> \(\Delta BDE\) vuông tại D

=> BD² + ED² = BE² ( Py-ta-go )      (3)

Từ (1),(2),(3) => IA² + IB² + IC² + ID² = BE²

                          => IA² + IB² + IC² + ID²= 4R² ( do BE = 2R )   (đpcm)

 

Answer 9

a) Xét (O): có góc BAE bội tiếp chắn nửa đường tròn (O)
=> góc BAE = 90 độ
=> AE vuông góc với AB tại A 
Mad CD vuông góc với AB tại I
=> CD//AE ( định lí từ vuông góc tới song song )
Xét (O) có 2 cung AC với ED chắn 2 dây AE//CD
=> cung AC= cung ED 
=> AC=ED

 

Answer 10

a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O)

⇒ góc BAE = 90 độ.

⇒ AE vuông góc với AB tại A

Mà CD vuông góc với AB tại I (GT)

⇒AE// CD ( định lí từ vuông góc đến song song)

- Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD.

⇒ cung AC = cung ED

⇒ AC = ED ( theo định lí giữa cung và dây cung )

b) CM được góc BDE = 90 độ

⇒ ED^2 + DB^2 = BE^2

⇒ AC^2 + ( IB^2 + ID^2 ) = ( 2R )^2 . ( vì ED = AC, định lí Pytago cho△BID vuông tại I )

⇒( IA^2 + IC^2 ) + ( IB^2 + ID^2 ) = 4R^2. ( định lí Pytago cho△ AIC vuông tại I )

 ⇒ Đcpcm

 a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O)

⇒ góc BAE = 90 độ.

⇒ AE vuông góc với AB tại A

Mà CD vuông góc với AB tại I (GT)

⇒AE// CD ( định lí từ vuông góc đến song song)

- Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD.

⇒ cung AC = cung ED

⇒ AC = ED ( theo định lí giữa cung và dây cung )

b) CM được góc BDE = 90 độ

⇒ ED^2 + DB^2 = BE^2

⇒ AC^2 + ( IB^2 + ID^2 ) = ( 2R )^2 . ( vì ED = AC, định lí Pytago cho△BID vuông tại I )

⇒( IA^2 + IC^2 ) + ( IB^2 + ID^2 ) = 4R^2. ( định lí Pytago cho△ AIC vuông tại I )

 ⇒ Đpcm

Answer 11

a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O)

⇒ góc BAE = 90 độ.

⇒ AE vuông góc với AB tại A

Mà CD vuông góc với AB tại I (GT)

⇒AE// CD ( định lí từ vuông góc đến song song)

- Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD.

⇒ cung AC = cung ED

⇒ AC = ED ( theo định lí giữa cung và dây cung )

b) CM được góc BDE = 90 độ

⇒ ED^2 + DB^2 = BE^2

⇒ AC^2 + ( IB^2 + ID^2 ) = ( 2R )^2 . ( vì ED = AC, định lí Pytago cho△BID vuông tại I )

⇒( IA^2 + IC^2 ) + ( IB^2 + ID^2 ) = 4R^2. ( định lí Pytago cho△ AIC vuông tại I ) (đpcm)

 

Answer 12

a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O) góc BAE = 90 độ. AE vuông góc với AB tại A Mà CD vuông góc với AB tại I (GT) » AE// CD ( định lí từ vuông góc đến → song song) - Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD. = cung AC = cung ED → AC = ED ( theo định lí giữa cung và dây cung ) b) CM được góc BDE = 90 độ ED^2 + DB^2 = BE^2 AC^2 + (IB^2 + ID^2) = (2R)^2. ( vì ED = AC, định lí Pytago cho – BID vuông tại I ) → (IA^2 + IC^2)+ (IB^2 + ID^2) = 4R^2. ( định lí Pytago cho A AIC vuông tại I) Đcpcm

Answer 13

a)

Answer 14

 

Answer 15

  

Answer 16

a) Có BAE=90 độ (góc nội tiếp chắn nửa đt) =>EA vuông AB
,à CD cuông AB (gt)
=>AE//CD (từ vg->//)
=>Cung AC ằng cung DE (đl hai cung giữ hai đth //)=>AC=AE (đpcm)
b) Có ΔAIC và ΔBDI vuông ở I => IA² + IB² + IC² + ID² = (IA² +IC²) + (IB² + ID²)= AC² + BD²=ED²+BD²=BE² (Pytago; góc EDB= 90 độ vì chắn nửa đt)
mà BE² = (2R)²=4R² nên IA² + IB² + IC² +ID² = 4R² (đpcm)

Answer 17

a)

Answer 18

Answer 19

Answer 20

a.Xét tam giác EBD có:Eb là đường kính=>tam giác EDB vuông tại D

Xét tam giác EBD và tam giác CBI có:

góc EDB=góc CIB=90 độ

góc DEB=góc ICB(cùng chắn cung BD)

=>tam giác EBD đồng dạng tam giác CBI

=>góc DBE=góc ABC(2 góc tương ứng)

=>AC=DE

b.Áp dụng đ/lý Py-ta-go vào tam giác vuông AIC ta có:

IA²+IC²=AC²

Mà AC=DE=>AC²=DE²

Áp dụng đ/lý Py-ta-go vào tam giác vuông DIB ta có:

ID²+IB²=BD² 

Áp dụng đ/lý Py-ta-go vào tam giác vuông EDB ta có:

ED²+BD²=EB²=(2R)²=4R²

Vậy IA²+IB²+IC²+ID²=4R²

Answer 21

a) Xét đường tròn (O) có $\widehat{AEB}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat{AEB}={90}^0$ hay $AE\perp AB$ mà $CD\perp AB$ nên $AE//CD$ suy ra $cungAC=cungED\Rightarrow AC=ED$ b) $\begin{array}{c}I{A}^2+I{C}^2=A{C}^2\left(Pytago\right)\\ \Rightarrow I{A}^2+I{C}^2=D{E}^2\left(doAC=DE\right)\\ màI{D}^2+I{B}^2=B{D}^2\left(Pytago\right)\\ lạicó\widehat{BDE}={90}^0\\ \Rightarrow I{A}^2+I{B}^2+I{C}^2+I{D}^2=D{E}^2+B{D}^2=B{E}^2={\left(2R\right)}^2\\ \Rightarrow I{A}^2+I{B}^2+I{C}^2+I{D}^2=4R^2\end{array}$

Answer 22

a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O)

⇒ góc BAE = 90 độ.

⇒ AE vuông góc với AB tại A

Mà CD vuông góc với AB tại I (GT)

⇒AE// CD ( định lí từ vuông góc đến song song)

- Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD.

⇒ cung AC = cung ED

⇒ AC = ED ( theo định lí giữa cung và dây cung )

b) CM được góc BDE = 90 độ

⇒ ED^2 + DB^2 = BE^2

⇒ AC^2 + ( IB^2 + ID^2 ) = ( 2R )^2 . ( vì ED = AC, định lí Pytago cho△BID vuông tại I )

⇒( IA^2 + IC^2 ) + ( IB^2 + ID^2 ) = 4R^2. ( định lí Pytago cho△ AIC vuông tại I )

 ⇒ Đcpcm

Answer 23

  

Answer 24

 

Answer 25

a) ΔABE có BE là đường kính => ΔABE vuông tại A=>\(AE\perp AB\) có \(AB\perp CD\)=> AE//CD=>AC=DE (liên hệ giữa cung và dây)

b) Xét ΔEDB có góc EDB=90 độ (góc nội tiếp chắn nửa đường tròn)=> ΔEDB vuông tại D

Áp dụng định lí Py-ta-go ta có:

ΔIAC có góc AIC=90 độ(\(CD\perp AB\))=>IA²+IC²=AC² mà AC=DE=>IA²+IA²=DE² (1)

ΔIBD có góc BID=90 độ (\(CD\perp AB\))=>IB²+ID²=BD²(2)

ΔEBD vuông tại D=>ED²+BD²=BE² lại có BE=2R

 Từ (1) và (2) suy ra:IA²+IB²+IC²+ID²=BE²=(2R)²=4R²

Answer 26

 

Answer 27

a) Xét (O) có : góc BAE nội tiếp chắn nửa đường tròn (O)

⇒ góc BAE = 90 độ.

⇒ AE vuông góc với AB tại A

Mà CD vuông góc với AB tại I (GT)

⇒AE// CD ( định lí từ vuông góc đến song song)

- Xét (O) có 2 cung AC và ED chắn 2 dây AE//CD.

⇒ cung AC = cung ED

⇒ AC = ED ( theo định lí giữa cung và dây cung )

b) CM được góc BDE = 90 độ

⇒ ED^2 + DB^2 = BE^2

⇒ AC^2 + ( IB^2 + ID^2 ) = ( 2R )^2 . ( vì ED = AC, định lí Pytago cho△BID vuông tại I )

⇒( IA^2 + IC^2 ) + ( IB^2 + ID^2 ) = 4R^2. ( định lí Pytago cho△ AIC vuông tại I )

 ⇒ Đcpcm

Answer 28

a) vì AE//CD

=>AE=CD

b)IA^2 + IC=AC^2=DE^2

IB^2+ID^@=BD^2

Answer 29

a) ^EAB là góc nội tiếp chắn nửa đường tròn nên ^EAB = 90⁰ hay AE⊥AB

Có AE⊥AB (cmt) và CD⊥AB (gt) nên AE//CD => Cung AC bằng cung DE hay AC = DE (đpcm)

b) ∆AIC và ∆BID vuông tại I nên IA² + IB² + IC² + ID² = (IA² + IC²) + (IB² + ID²) = AC² + BD² = ED² + BD² = BE² (∆EDB có ^EDB = 90⁰ do nó là góc nội tiếp chắn nửa đường tròn)

Mà BE² = (2R)² = 4R² nên IA² + IB² + IC² + ID² = 4R² (đpcm)

 

Answer 30

a) ^EAB là góc nội tiếp chắn nửa đường tròn nên ^EAB = 90⁰ hay AE⊥AB

Có AE⊥AB (cmt) và CD⊥AB (gt) nên AE//CD => Cung AC bằng cung DE hay AC = DE (đpcm)

b) ∆AIC và ∆BID vuông tại I nên IA² + IB² + IC² + ID² = (IA² + IC²) + (IB² + ID²) = AC² + BD² = ED² + BD² = BE² (∆EDB có ^EDB = 90⁰ do nó là góc nội tiếp chắn nửa đường tròn)

Mà BE² = (2R)² = 4R² nên IA² + IB² + IC² + ID² = 4R² (đpcm)