Cho đường tròn (O; R) đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến d và d' với (O). Một đường thẳng qua O cắt d ở M và cắt d' ở P. Từ O vẽ một tia vuông góc với MP và cắt d' ở N
a, Chứng minh OM = OP và tam giác NMP cân
b, Gọi I là hình chiếu vuông góc của O lên MN. Chứng minh OI = R và MN là tiếp tuyến của (O)
c, Chứng minh AM. BN = R 2
d, Tìm vị trí của M để tứ giác AMNB có diện tích đạt giá trị nhỏ nhất
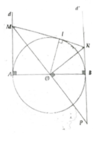
a, ∆MAO = ∆PBO => MO = OP => ∆MNP cân
Vì đường cao NO đồng thời là đường trung tuyến
b, 1 O I 2 - 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => OI = R
=> MN là tiếp tuyến của (O)
c, AM.BN = MI.IN = O I 2 = R 2
d, S A M N B = M N . A B 2
=> S A M N B min
<=> M N m i n <=> AM = R











