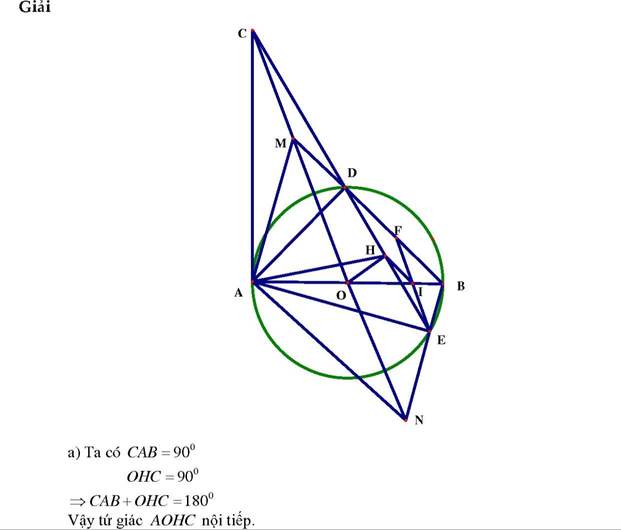
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp tuyến). Qua C thuộc tia Ax, vé đường thẳng cắt đường tròn (O) tại hai điểm D và Eb(D nằm giữa C và E; D và E nằm về phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.Đường thẳng cắt tia BD,BE lần lượt tại M và N
Đã chứng minh: tứ giác AOHC nội tiếp,AC. AE = AD. CE
Cần chứng minh: AM//BN
Cần gấp!!!!
Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F.
Suy ra: Góc HEI = góc HCO
Vì tứ giác AOHC nội tiếp nên:
Góc HAO= góc HEI= góc HCO
<=> Tứ giác AHIE nội tiếp suy ra: góc IHE= góc IAE= góc BDE
=> HI//BD
Mà H là trung điểm của DE
=> I là trung điểm của EF.
Ta có: EF//MN và IE=IF
=> O là trung điểm của đoạn thẳng MN (1)
Từ (1) suy ra:
Tứ giác AMBN là hình bình hành => AM//BN(₫pcm)
Cái này mới T/khảo nek:))
THAM KHẢO