Các câu hỏi tương tự
Cho 2 đường tròn đồng tâm, tâm O bán kính R và tâm O bán kính R' (R>R'). Điểm M nằm ngoài 2 đường tròn. Vẽ MA là tiếp tuyến của đường tròn tâm O bán kính R. MB là tiếp tuyến của đường tròn tâm O bán kính R'. Chứng minh rằng đường trung trực của đoạn thẳng AB đi qua trung điểm của OM
Cho nửa đường tròn tâm O, đường kính AB. Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn. Vẽ bán kính OE (E thuộc 1/2(O),E khác A,B). Tiếp tuyến của nửa đường tròn tại E cắt Ax, By lần lượt tại C và D.a, Cm AC+BDCDb, góc COD 90°c, Gọi I là giao của OC và EA, K là giao của OD và BE. Tứ giác EIOK là hình gì? Vì sao?d, Xác định vị trí của bán kính OE để tứ giác EIOK là hình vuông.GIÚP MÌNH NHÉ!
Đọc tiếp
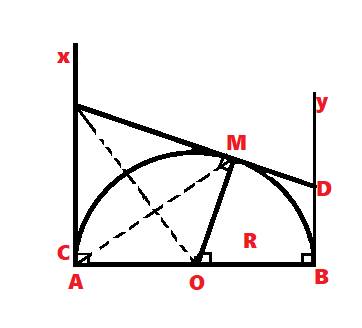
Cho nửa đường tròn tâm O, đường kính AB. Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn. Vẽ bán kính OE (E thuộc 1/2(O),E khác A,B). Tiếp tuyến của nửa đường tròn tại E cắt Ax, By lần lượt tại C và D.
a, Cm AC+BD=CD
b, góc COD = 90°
c, Gọi I là giao của OC và EA, K là giao của OD và BE. Tứ giác EIOK là hình gì? Vì sao?
d, Xác định vị trí của bán kính OE để tứ giác EIOK là hình vuông.
GIÚP MÌNH NHÉ!
Lấy điểm A trên (O;R),vẽ tiếp tuyến Ax . Trên Ax lấy điểm B ,trên (O;R) lấy điểm C sao cho BC=AB
a, CMR : CB là tiếp tuyến của (O)
b, Vẽ đường kính AD của (O),kẻ CK vuông góc với AD.
c,Lấy M trên cung nhỏ AC của (O) ,vẽ tiếp tuyến tại M cắt AB,AC lần lượt tại E,F.Vẽ đường tròn tâm I nội tiếp tam giác BFE.CMR:tam giác MAC đồng dạng vs tam giác IFE
Giải giúp tớ với, cần câu trả lời gấp ạk, thanks1 / Cho tam giác ABC, góc A90 độ, AC3AB. D, E thuộc AC sao cho ADDEEC.a/ Gọi M là điểm đối xứng với B qua D. Chứng minh rằng ABCM là tứ giác nội tiếpb/ Chứng minh rằng góc ACB+ góc AEB 45 độ2/ Cho đường tròn tâm O bán kính R3cm và một điểm S cố định bên ngoài đường tròn sao cho SO5cm. Vẽ tiếp tuyến SA với A là tiếp điểm và cát tuyến SCB không qua tâm sao cho O nằm trong góc ASB ( C nằm giữa S...
Đọc tiếp
Giải giúp tớ với, cần câu trả lời gấp ạk, thanks
1 / Cho tam giác ABC, góc A=90 độ, AC=3AB. D, E thuộc AC sao cho AD=DE=EC.
a/ Gọi M là điểm đối xứng với B qua D. Chứng minh rằng ABCM là tứ giác nội tiếp
b/ Chứng minh rằng góc ACB+ góc AEB= 45 độ
2/ Cho đường tròn tâm O bán kính R=3cm và một điểm S cố định bên ngoài đường tròn sao cho SO=5cm. Vẽ tiếp tuyến SA với A là tiếp điểm và cát tuyến SCB không qua tâm sao cho O nằm trong góc ASB ( C nằm giữa S và B ). Gọi H là trung điểm của CB
a) Chứng minh rằng tứ giác SAOH nội tiếp một đường tròn
b) Tính chu vi và diện tích của đường tròn ngoại tiếp tứ giác SAOH
c) Tính tích SC.SB
3/ Cho tam giác ABC nội tiếp đường tròn tâm O đường kính AB=2R. Lấy H là trung điểm của dây BC. Tia OH cắt đường tròn tại D, AD lần lượt cắt tiếp tuyến Bx của đường tròn tại E và F
a) Chứng minh AD là tia phân giác của góc CAB
b) Chứng minh tứ giác ECDF là tứ giác nội tiếp
c) Cho CD= R=căn10cm. Tính diện tích của hình viên phân giới hạn bởi cung CDB với dây CB
4/ Cho tam giác ABC cân ở A nội tiếp đường tròn O đường kính I. Gọi E là trung điểm của AB. K là trung điểm của OI. Chứng minh rằng AEKC là tứ giác nội tiếp
5/Cho tam giác ABC. Các đường phân giác trong của B, C cắt nhau tại S, các đường phân giác ngoài của B và C cắt nhau tại E. Chứng minh rằng BSCE là 1 tứ giác nội tiếp.
Cho tam giác ABC có AB = 3,59; BC = 4,90; CA = 5,74, đường cao BH. Trên cạnh BC lấy điểm M sao cho MC = 2MB. Gọi I là giao điểm của AM và BH, r là bán kính đường tròn nội tiếp tam giác IBM, R là bán kính đường tròn ngoại tiếp tam giác IBM. Tính giá trị của r + R (Làm trên kết quả đến 3 chữ số ở phần thập phân)
Chứng minh giúp mình câu c với ạCho nửa đường tròn tâm O bán kính R, đường kính AB. Kẻ tiếp tuyến Ax, By. Từ M trên đường tròn kẻ tiếp tuyến thứ ba cắt Ax tại C, cắt By tại D.a. Chứng minh OC ⊥ AMb. Chứng minh A, C, M, O cùng thuộc một đường trònc. AC . BD R
Đọc tiếp
Chứng minh giúp mình câu c với ạ
Cho nửa đường tròn tâm O bán kính R, đường kính AB. Kẻ tiếp tuyến Ax, By. Từ M trên đường tròn kẻ tiếp tuyến thứ ba cắt Ax tại C, cắt By tại D.
a. Chứng minh OC ⊥ AM
b. Chứng minh A, C, M, O cùng thuộc một đường tròn\(\)
c. AC . BD = R
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.a, cho biết R5cm, OM3cm. Tính độ dài dây EH.b, Chứng minh AH là tiếp tuyến đường tròn(O)c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tu...
Đọc tiếp
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.
a, cho biết R=5cm, OM=3cm. Tính độ dài dây EH.
b, Chứng minh AH là tiếp tuyến đường tròn(O)
c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.
d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tuyến thứ 2 với đường tròn(O), cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q. Chứng minh AE=DQ
1. Cho 2 đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC ($Bin (O), Cin (O)$)a. Tính góc BACb. Tính BC.c. Gọi D là gđ của CA với đường tròn (O) (D khác A). CMR 3 điểm B,O,D thẳng hàngd. Tính BA, CA2. Cho đ B nằm giữa A và Csao cho AB14cm, BC28cm. Vẽ về 1 phía của AC các nửa đường tròn tâm I,K,O có đường kính theo thứ tự AB, BC, AC.Tính bán kính đường tròn (M) tiếp xúc ngoài với các nửa đường tròn (I), (K), và tiê...
Đọc tiếp
1. Cho 2 đường tròn (O;R) và (O';r) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC ($B\in (O), C\in (O')$)
a. Tính góc BAC
b. Tính BC.
c. Gọi D là gđ của CA với đường tròn (O) (D khác A). CMR 3 điểm B,O,D thẳng hàng
d. Tính BA, CA
2. Cho đ B nằm giữa A và Csao cho AB=14cm, BC=28cm. Vẽ về 1 phía của AC các nửa đường tròn tâm I,K,O có đường kính theo thứ tự AB, BC, AC.Tính bán kính đường tròn (M) tiếp xúc ngoài với các nửa đường tròn (I), (K), và tiếp xúc trong với nửa đường tròn (O).
3. Cho đường tròn (O) nội tiếp tam giác đều ABC. 1 tiếp tuyến của đường tròn cắt AB, AC theo thứ tự ở M và N.
a. Tính diện tích AMN biết BC=8cm, MN=3cm
b. CMR: $MN^2=AM^2+AN^2-AM.AN$
c*. Chứng minh rằng: $\frac{AM}{MB}+\frac{AN}{NC}=1$
Cho nửa đường tròn (o)bán kính an vẽ các tiếp tuyến ax by về nửa mặt phẳng bờ ab chứa nửa đg tròn trên ax và by theo thứ tự lấy m và n sao cho góc MON bằng 90° gọi I là của MN chứng minh rằng:
a,AB là tiếp tuyến của đg tròn(I;IO)
B,MO là tia phân giác của góc AMN










