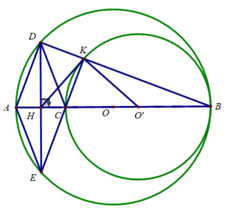
c) Ta có:
∠(CKB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O')) ⇒ CK ⊥ BD
∠(ADB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O)) ⇒ AD ⊥ BD
⇒ CK // AD
Lại có: CE // AD (Tứ giác ADCE là hình thoi)
⇒ C, E, K thẳng hàng
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB. Gọi K là giao điểm của DB với đường tròn (O’). Chứng minh rằng ba điểm E, C, K thẳng hàng.
Cho đường tròn (O) đường kính AB và C là điểm nằm giữa A và O. Vẽ đường tròn (I) có đường kính CB
a, Xét vị trí tương đối của (O) và (I)
b, Kẻ dây DE của (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì?
c, Gọi K là giao điểm của đoạn thẳng DB và (I). Chứng minh ba điểm E, C, K thẳng hàng
d, Chứng minh HK là tiếp tuyến của (1)
Cho đường tròn (O), đường kính AB .Gọi C là điển nằm giữa A và O. Vẽ đường tròn (I) có đường kính CB
a) Xét vị trí tương đối của hai đường tròn (O) và (I)
b) Kẻ dây CE của đường tròn O vuông góc với AC tại trug điểm H của AC. Tứ giác ADCE là hình gì?Tại sao
c) Gọi K là giao điểm DB và đường tròn (I). Cm 3 điểm E,C,K thẳng hàng
d) Cm HK là tiếp tuyến của đường tròn (I)
GIÚP VỚI
Cho đường tròn (o) đường kính AB , điểm C nằm giữa A và O . Vẽ đường tròn (o') đường kính BC
a) xác định vị trí tương đối của đường tròn (o) và (o')
b) kẻ dây DE của đường tròn (o) vuông góc với AC tại trung điểm H của AC . Tứ giác ADCE là hình j ? Vì sao.
c) gọi K là giao điểm của DB và (o'). CMR 3 điểm E,C,K thẳng hàng
d) CMR: HK là tiếp tuyến của đường tròn (o)
Cho đường tròn (O) đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) đường kính BC. Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC.
a) Tứ giác ADCE là hình gì? Vì sao?
c) gọi K là giao điểm của DB và (O’). CMR: 3 điểm E, C, K thẳng hàng
Cho tam giác ABC có góc A nhỏ hơn 90 độ .Vẽ đường tròn (O) đường kính AB và đường tròn (O') đường kính AC.Đường thẳng AB cắt đường tròn (O')tại điểm thứ hai là D ,đường thẳng AC cắt đường tròn (O')tại điểm thứ hai là E.
a]Chứng minh bốn điểm B,C,D,E cùng năm trên một đường tròn
b]Gọi F là giao điểm của hai đường tròn (O) và (O') (F khác A).Chứng minh 3 điểm B,F,C thẳng hàng và FA là phân giác của góc EFD.
c]Gọi H là giao diểm của AB và EF .Chứng minh BH.AD=AH.BD
Cho đường tròn tâm O đường kính AB và điểm C thuộc đường kính AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Đường thẳng vuông góc với AB tại C cắt (O) tại D và E. Gọi M, N thứ tự là giao điểm thứ 2 của (I) với DA, của (K) với DB.
Trong trường hợp (O) giao đường tròn ngoại tiếp ∆ CDM tại điểm thứ 2 là P khác D. CMR: đường thẳng PD, MN, AB đồng quy.
cho đường tròn tâm O đường kính AB ,điểm m thuộc đọan AB,qua m vẽ đường thẳng d vuông góc với AB.Trên d lấy C sao cho C nằm ngoài đường tròn tâm O .Vẽ các tiếp tuyến CE CF với đường tròn tâm O.gọi h,k là giao điểm của CA,CB với đường tròn tâm O (H khác A,K khác B);I là giao điểm của AK và BH.
Chứng minh C M E F O thuộc 1 đường tròn
Chứng minh E F I thẳng hàng
Xác định vị trí điểm C để tâm đường tròn ngoại tiếp tam giác ABC nằm trên đường thẳng EF
Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME<MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).
a. Chứng minh rằng MA.MB = ME.MF
b. Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.
c. Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.
d. Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng.
