⇒ D nằm trên cung chứa góc 30 ° dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30 ° dựng trên BC.
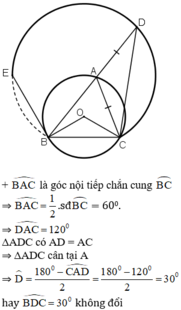
Cho đường tròn (O), cung BC có số đo bằng 120 ° , điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC. Hỏi điểm D di chuyển trên đường nào?
cho dường tròn O có cung BC=120 độ .lấy điểm D trên tia đối của AB sao cho AD=AC. hỏi D di chuyển trên Đường nào
Cho đường nửa tròn tâm O, đường kính AB. Các điểm C và D thuộc cung AB sao cho sđ cung CD=90 độ(C thuộc cung AD). Gọi E là giao điểm cỉa AC và BD, K là giao điểm của AD và BC.
Khi cung CD di chuyển trên nửa đường tròn thì điểm K di chuyển trên đường nào?
Mọi người ơi giúp e vs s, nghĩ mãi mà không ra :V Đề bài : Cho nửa đường tròn tâm O đường kính BC lấy điểm A trên cung BC sao cho AB<AC , D là trung điểm OC từ D kẻ đường vuông góc với BC cắt AC tại E
a, tứ giác ABDE nội tiếp được đường tròn , xác định tâm
b, CM góc BAD = góc BED
c, CM CE.CA = CD.CB
d, trên tia đối của tia AB lấy M sao cho AM = AC . Giả sử không có điều kiện AB<AC , tìm quỹ tích điểm M khi A di chuyển trên nửa đường tròn tâm O.
Cho đường tròn ( O;R ) và dây BC < 2R. A di chuyển trên cung lớn BC sao cho AC > BC. Gọi D là điểm chính giữa cung nhỏ BC. Các tiếp tuyến của ( O ) tại D và C cắt nhau tại E. Tia AB cắt tia CD tại P, tại AD cất tia CE tại Q. AD cắt BC tại K.
1. CM tứ giác APQC nội tiếp
2. CMR AK.AD không đổi khi A di chuyển trên cung lớn BC.
3/ CMR PQ // BC và \(\frac{1}{CE}=\frac{1}{CQ}+\frac{1}{CK}\)
Cho đường tròn (O:R) có AB là 1 dây cố định (AB<2R) .Trên cung lơn sAB lấy hai điểm C và D sao cho AD//BC
a, kẻ tt tại A và D chứng minh AODI nội tiếp
b,Gọi M là giao điểm của AC và BD .CM M thuộc 1 đường tròn cố định khi C ,D di chuyển trên cung lớn AB sao cho AD//BC
c.Cho biết AB=R căn 2 và BC=R.Tính S ABCD theo R
Giải bài toán hình Cho (O) đường kính BC và một điểm A nằm trên cung BC sao cho AB>AC.Trên tia AC lấy điểm D sao cho AD=AB, vẽ hình vuông BADE,tia AE cắt (O) tại điểm thứ hai F. a) Cm tam giác FBC vuông cân b) Cm FC=FD d)Khi A di động thì E chạy trên đường nào
cho đường tròn (ở,r)trên đường tròn o lấy ba điểm A,B,C ,sao cho tam giác ABC đều .vẽ đường kính AI ,D là một điểm di động nằm trên cung nhỏ AC của ô;(D khác A và C
a)c/m AI là tia phân giác của góc BAC
b)từ C vẽ đường thẳng vuông góc với DI ,đường thẳng này cắt DB tại E .c/m CE=DE
C) khi D di chuyển trên cung nhỏ AC và A,B,C.(O) cố định thì E di chuyển trên đường nào
Cho đường tròn (O;R) có AB là một dây cố định (AB < 2R) . Trên cung lớn AB lấy 2 điếm C ; D sao cho AD // BC
a) Kẻ các tiếp tuyến với đường tròn (O;R) tại A ; D , chúng cắt nhau tai I . Chứng minh AODI là tứ giác nội tiếp .
b) Gọi M là giao điểm của AC và BD . Chứng minh rằng điểm M thuộc đường tròn cố định khi C ; D di chuyển trên cung lớnn AB sao cho AD //BC
c) Cho biết AB = R và BC = R . Tính điện tích tứ giác ABCD theo R
