ΔAHB vuông nên AE.AB = AH2
ΔAHC vuông nên AF.AC = AH2
Suy ra AE.AB = AF.AC
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
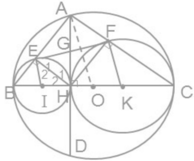
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Tứ giác AEHF là hình gì? Vì sao?
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Xác định vị trí của điểm H để EF có độ dài lớn nhất
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.a) Chứng minh đẳng thức AE.AB AF.ACb) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)c) Xác định vị trí của điểm H để EF có độ dài lớn nhất.Các bạn giải giúp mình nha, mình chuẩn bị kiểm định nên cần gấp ạ, cảm ơn mọi người.
Đọc tiếp
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.
Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
a) Chứng minh đẳng thức AE.AB = AF.AC
b) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)
c) Xác định vị trí của điểm H để EF có độ dài lớn nhất.
Các bạn giải giúp mình nha, mình chuẩn bị kiểm định nên cần gấp ạ, cảm ơn mọi người.
11 tháng 2 2022 lúc 19:43
Cho đường tròn (O) có đường kính BC, dây AD vuông với BC tại H. Gọi E,F theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC. Gọi (I);(K) theo thứ tự các đường tròn ngoại tiếp tam giác HBE; HCF.
a) Hãy xác định vị chí tương đối của các đường tròn (I) ; (O) và (K).
b) Tứ giác AEHF là hình gì ? vì sao?
c) Chứng minh đẳng thức AE . AB= AF . AC
Giúp mình bài này với ạ Cho đường tròn tâm (O) đường kính BC,dây AD vuông góc với BC tại H. Gọi E,F theo thứ tự là chân đường vuông góc kẻ từ H đến AB,AC.Gọi (I) (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE,HCF. a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K). b) tứ giác AEHF là hình gì? vì sao? c) chứng minh đẳng thức AE.ABAF.AC d) chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K) e) xác định vị trí của điểm H để EF có độ...
Đọc tiếp
Giúp mình bài này với ạ
Cho đường tròn tâm (O) đường kính BC,dây AD vuông góc với BC tại H. Gọi E,F theo thứ tự là chân đường vuông góc kẻ từ H đến AB,AC.Gọi (I) (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE,HCF.
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).
b) tứ giác AEHF là hình gì? vì sao?
c) chứng minh đẳng thức AE.AB=AF.AC
d) chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)
e) xác định vị trí của điểm H để EF có độ dài lớn nhất.
Giúp mình giải câu d) và e) với, mình cảm ơn
Cho tam giác ABC ngoại tiếp đường tròn (O). Gọi D, E, F theo thứ tự là tiếp điểm trên các cạnh BC, AB, AC. Gọi H là chân đường vuông góc kẻ từ D đến EF. Chứng minh rằng góc BHE bằng góc CHF
Cho ∆ABC có 3 góc nhọn (AB < AC). Đường tròn đường kính BC cắt AB, AC theo thứ tự tại E và F. Biết BF cắt CE tại H và AH cắt BC tại D a) C/M tứ giác BEFC nội tiếp và AH vuông góc với BC b) C/M AE.AB = AF.AC c) Gọi O là tâm đường tròn ngoại tiếp ∆ABC và K là trung điểm của BC. Tính tỉ số OK/OC khi tứ giác BHOC nội tiếp Giúp mik câu c vs ạ