Cho đoạn thẳng MN = 6 cm. Trên tia MN lấy điểm P sao cho MP = 1 cm, trên tia NM lấy điểm Q sao cho NQ = 1 cm. Khi đó:
A. MQ = NP
B. Đường trung trực của đoạn thẳng MN vuông góc với đoạn thẳng PQ
C. Đường trung trực của đoạn thẳng MN trùng với đường trung trực của đoạn thẳng PQ
D. Cả A, B, C đều đúng
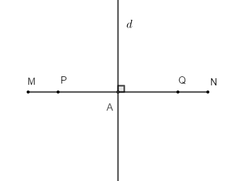
+ Trên tia MN có:
MN = 6 cm; MP = 1 cm
Suy ra P nằm giữa M và N (do 6 > 1)
⇒ MP + PN = MN ⇒ PN = MN – MP = 6 – 1 = 5 cm
+ Trên tia NM có:
NM = 6 cm; NQ = 1 cm
Suy ra Q nằm giữa M và N (do 6 > 1)
⇒ NQ + QM = NM ⇒ QM = NM – NQ = 6 – 1 = 5 cm
Do đó: PN = QM (= 5 cm) A đúng
+ Gọi A là trung điểm của đoạn thẳng MN ⇒ AM = AN = 1/2 MN = 3 cm
Gọi d là đường thẳng đi qua A và vuông góc với MN tại A
Do đó d là đường trung trực của đoạn thẳng MN
Vì P và Q đều thuộc MN, nên suy ra d ⊥ PQ (1) ⇒ B đúng
+ Trên tia MN có MA = 3 cm; MP = 1 cm
Suy ra P nằm giữa M và A ⇒ MP + PA = MA ⇒ PA = MA – MP = 3 – 1 = 2 cm
Chứng minh tương tự ta có: NQ + QA = NA ⇒ QA = NA – NQ = 3 – 1 = 2 cm
Do đó: PA = QA, mà P, Q, A thẳng hàng (do P, Q, A đều thuộc MN)
Suy ra A là trung điểm của PQ (2)
Từ (1) và (2) suy ra d là đường trung trực của đoạn thẳng PQ ⇒ C đúng
Chọn đáp án D










