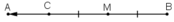
– Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy 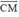 và
và 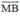 cùng hướng nên
cùng hướng nên 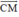 =
= 
Khi đó:
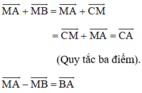
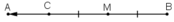
– Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy 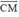 và
và 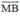 cùng hướng nên
cùng hướng nên 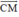 =
= 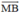
Khi đó:
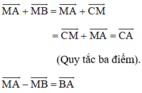
Cho đoạn thẳng AB và điểm M nằm giữa hai điểm A và B. khẳng định nào sau đây là đúng?
A. A M → . A B → = − A M . A B
B. A M → . A B → = A M . A B
C. A M → . A B → < 0
D. A M → . A B → > A M . A B
Cho đoạn thẳng AB và điểm M nằm giữa hai điểm A và B. khẳng định nào sau đây là đúng?
A. M A → . M B → > 0
B. M A → . M B → < − M A . M B
C. M A → . M B → = − M A . M B
D. M A → . M B → = M A . M B
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy điểm N sao cho IN = MI
a) CMR: \(\overrightarrow{BN}-\overrightarrow{BA}=\overrightarrow{MB}\)
b) Tìm các điểm D, C sao cho: \(\overrightarrow{NA}+\overrightarrow{NI}=\overrightarrow{ND}\) ; \(\overrightarrow{NM}-\overrightarrow{BN}=\overrightarrow{NC}\)
Bài 5: (3,0 điểm) Cho tam giác ABC cân tại A, A là góc nhọn. M là trung điểm BC. Gọi D là điểm nằm giữa A và M.
a) Cho AC = 10cm, AM = 8cm. Tính độ dài cạnh BC
b) Vẽ đường thẳng d đi qua D và song song với BC, Vẽ đường thẳng đi qua B song song với AC và cắt d tại E, vẽ đường thẳng đi qua C song song với AB và cắt d tại F. Chứng minh tam giác AEF là tam giác
cho đường tròn O,R và điểm M nằm ngàoi O qua M kẻ tiếp tuyeens MA MB với O và cát tuyến MDC sao cho MC<MD đoạn thẳng MO cắt AB tại H
a chứng minh MAOB nôi tiếp
b cm MB^2=MC.MD
c chứng minh CHOD nội tiếp HA là phân giác CHD
d giả sử M cđ chứng minh MCD thay đổi trọng tâm G của tam giác BCD thuộc 1 đường tròn cố định
Câu 4(1,5điểm): Cho hình vuông ABDC tâm O cạnh bằng a.
a) Tính độ dài của :vector BD– vector BC.
b) Chứng minh: vector MA+vector MB+ vector MC+vector MD=4 vector MO
c) Tìm tập hợp tất cả các điểm M sao cho |vector MA+vector MB+vector MC|=1.
Cho đường tròn (O) và các điểm M, N thuộc (O) sao cho \(\widehat{MON=90}\)với P là điểm thuộc đoạn OM sao cho \(OM=\sqrt{7}OP\)và Q là điểm thuộc đoạn QN. Đường thẳng PQ cắt (O) tại A, B ( P nằm giữa A và Q )
CMR \(\frac{1}{3QP}=\frac{1}{PA}+\frac{1}{PB}\)
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn , vẽ các tiếp tuyến MA,MB với đường tròn (O) ,(AB là các tiếp điểm ) và cát tuyến MCD không đi qua tâm O(MC,<MD, A và O nằm khác phía có bờ la CD ),gọi I là trung điểm của CD
a. Chứng minh 5 điểm M,A,I,O,B cùng thuộc một đường tròn
b. Chứng minh MA2= MC.MD
Cho tứ giác ABCD. Gọi M,N là các điểm được xác định bởi MA- 2 MB = 0 , 2NC+3 NA = 0 và G là trọng tâm tam giác ABC
a/Chứng minh: AB+CD = AD+ CB .
b/ Tính AM theo AB và AN theo AC.
c/ Chứng minh ba điểm M,G, N thẳng hàng.