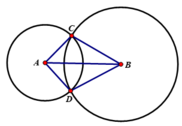
Nối BC, BD, AC, AD.
ΔABC và ΔABD có:
AC = AD (=2cm)
BC = BD (=3cm)
AB cạnh chung
Nên ΔABC = ΔABD (c.c.c)
Suy ra góc CAB = góc DAB (góc tương ứng)
⇒ AB là tia phân giác của góc CAD
Cho đoạn thẳng AB dài 4cm .Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm , chúng cắt nhau ở C và D .Chứng minh rằng AB là tia phân giác của góc CAD.
Cho đoạn thẳng AB dài 4cm. Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm, chúng cắt nhau ở C và D. Chứng minh AD là tia phân giác của góc CAD
cho đoạn thẳng ab dài 4cm.vẽ đường tròn tâm a bán kính 2cm và đường tròn tâm b bán kính 3cm chúng cắt nhau ở c và d .chứng minh rằng ab la tia phân giác góc cad
cho đoạn AB =cm. Vẽ đường tròn tâm A bán kính 2cmvà đường tròn tâm B bán kính 3cm , chúng cắt nhau tại C va D . chứng minh rằng AB là tia phân giác của góc CAD
Cho đoạn thẳng AB=4cm. Vẽ đường tròn tâm A bán kinh 2cm và đường tròn tâm B bán kính 3 cm chúng cắt nhau tại C và D. CMR: AB là tia phân giác của góc CAD.
Cho đoạn thẳng AB =4cm.Vẽ đường tròn tâm A bán kính 2cm,đường tròn tâm B bán kính 3cm,chúng cắt nhau tại C và D.Chứng minh rằng AB là tia P/g của góc CAD
Cho một đoạn thẳng AB dài 4 cm.Vẽ đường tròn tâm A bán kính 2 cm và đường tròn tâm B bán kính 3 cm,chúng cắt nhau ở C và D.Chứng minh rằng AB là tia phân giác của góc CAD.
Cho đoạn thẳng AB dài 4cm.Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm,chúng cắt nhâu ở C và D.CMR AB là tia phân giác của \(\widehat{CAD}\)
Cho đoạn thẳng AB=5cm. Vẽ đường tròn tâm A bán kinh 3cm và đường tròn tâm B bán kính 4 cm chúng cắt nhau tại C và D. CMR: AB là tia phân giác của góc CAD.
