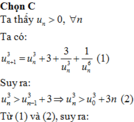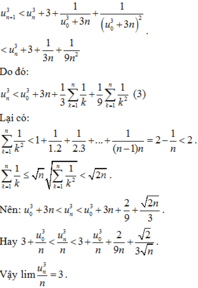Các câu hỏi tương tự
Cho dãy số
u
(
n
)
xác định bởi
u
(
1
)
1
;
u
(
m
+
n
)
u...
Đọc tiếp
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Cho dãy số xác định bởi u1=1 , u n+1 = \(2un+\frac{n-1}{n^2+3n+2}\). khi đó u 2018 bằng
Cho dãy số được xác định bởi: U1=12
\(\frac{2\cdot U_{n+1}}{n^2+5n+6}=\frac{U_n+n^2-n-2}{n^2+n}\)
Tìm số hạng tổng quát của dãy số
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
cho dãy số (un):\(\left\{{}\begin{matrix}u_1=2010\\u^2+2019u_n-2011u_{n+1}+1=0\end{matrix}\right.\)
tìm lim\(\left(\Sigma^n_{i=1}\dfrac{1}{u_i+2010}\right)\)
Cho dãy số u(n)=\(1/(2*4) +1/(5*7)+...+1/((3n-1)*(3n+1))\)
Tính Lim u(n).
Cho dãy số (un) được xác định bởi :
u
0
2011
u
n
+
1
u
n...
Đọc tiếp
Cho dãy số (un) được xác định bởi : u 0 = 2011 u n + 1 = u n 2 u n + 1 , ∀ n = 1 , 2 . . . Tìm phần nguyên của (un) với 0 ≤ n ≤ 1006.
A. [un] = 2014 – n
B. [un] = 2011 – n
C. [un] = 2013 – n
D. [un] = 2012 – n
cho dãy số \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{1}{2}\left(u^2_n+1\right)\end{matrix}\right.\) tìm lim\(\Sigma^n_{i=1}\dfrac{1}{u_i+1}\)