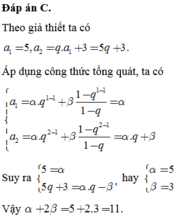Các câu hỏi tương tự
Cho dãy số (un)(un) có số hạng tổng quát un=−2n+3un=−2n+3 với n∈N∗n∈N∗ . Số hạng u5u5 bằng
A.
13.
B.
5.
C.
−7
D.
−10
Cho
P
:
x
+
y
-
z
-
1
0
và
Q
:
-
2
x
+
z
+
4
0
và
A
-
1
;
1
;
3
. Gọi
α
là mặt phẳng qua...
Đọc tiếp
Cho P : x + y - z - 1 = 0 và Q : - 2 x + z + 4 = 0 và A - 1 ; 1 ; 3 . Gọi α là mặt phẳng qua A, α ⊥ P , α ⊥ Q . Tìm một vectơ pháp tuyến n → của α .
![]()
![]()
![]()
![]()
Cho dãy số \(\left(u_n\right)\)thỏa mãn \(logu_1+\sqrt{2+logu_1-2logu_{10}}=2logu_{10}\)và\(u_{n+1}=2u_n\)với mọi \(n\ge1\).Giá trị nhỏ nhất của n để \(u_n>5^{100}\)?
Cho dãy un xác định bởi \(u_1=1\)và \(\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\).Chứng minh dãy đó có giới hạn và tìm giới hạn dãy đó
Cho x=N.b, với a là hằng số, N là số nguyên dương
Tính : ax+20a(x-b)+21a(x-2b)+22a(x-3b)+23a(x-4b)+...+2N-2[x-(N-1)b]
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y - 3z + 1 0; 4x - 2y + (
n
2
+ n)z - n 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau A. m-2 và n2 B. m2 và n-3 C. m-2 và n2 hoặc n-3 D. m-2 và n-3
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y - 3z + 1 = 0; 4x - 2y + ( n 2 + n)z - n = 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau
A. m=-2 và n=2
B. m=2 và n=-3
C. m=-2 và n=2 hoặc n=-3
D. m=-2 và n=-3
Trong không gian Oxyz cho các đường thẳng
d
1
:
x
+
2
y
-
3
z
+
1
0
2
x
-...
Đọc tiếp
Trong không gian Oxyz cho các đường thẳng d 1 : x + 2 y - 3 z + 1 = 0 2 x - 3 y + z + 1 = 0 và d 2 : x = 2 + a t y = - 1 + 2 t z = 3 - 3 t
Trong đó t là tham số, a là một số thực cho trước. Xác định a để tồn tại mặt phẳng (Q) chứa d 1 và vuông góc với d 2
A. a = -2
B. a = 2
C. a = -1
D. a = 1
Tính tổng A=12 + 22 + 32 + 42 + ... + N2
hay A=1 + 4 + 9 + 16 + ... + N2
Viết công thức tổng quát vd: n*n+1. (không dùng sigma)
Cho dãy số
(
a
n
)
thỏa mãn
5
a
n
+
1
-
a
n
3
3
n
+
2
với mọi n
≥...
Đọc tiếp
Cho dãy số ( a n ) thỏa mãn 5 a n + 1 - a n = 3 3 n + 2 với mọi n ≥ 1. Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 41
B. n = 39
C. n = 49
D. n = 123