Các câu hỏi tương tự
Bài 4: Tìm số dư của phép chia cho 9. CHIA9.PAS Cho một số nguyên dương N có M chữ số. Yêu cầu: Tìm số dư của phép chia số N cho 9. Dữ liệu vào: Cho trong file văn bản CHIA9.INP, có cấu trúc như sau: - Dòng 1: Ghi số nguyên dương M là số lượng chữ số của số N (1 ≤ M ≤ 100). - Dòng 2: Ghi M chữ số của số N, các chữ số được ghi liền nhau. Dữ liệu ra: Ghi ra file văn bản CHIA9.OUT, theo cấu trúc như sau: - Dòng 1: Ghi số nguyên dương Q, là số dư tìm được. Ví dụ: CHIA9.INP CHIA9.OUT 5 74283 6Bài 5:...
Đọc tiếp
Bài 4: Tìm số dư của phép chia cho 9. CHIA9.PAS Cho một số nguyên dương N có M chữ số. Yêu cầu: Tìm số dư của phép chia số N cho 9. Dữ liệu vào: Cho trong file văn bản CHIA9.INP, có cấu trúc như sau: - Dòng 1: Ghi số nguyên dương M là số lượng chữ số của số N (1 ≤ M ≤ 100). - Dòng 2: Ghi M chữ số của số N, các chữ số được ghi liền nhau. Dữ liệu ra: Ghi ra file văn bản CHIA9.OUT, theo cấu trúc như sau: - Dòng 1: Ghi số nguyên dương Q, là số dư tìm được. Ví dụ: CHIA9.INP CHIA9.OUT 5 74283 6
Bài 5: Tìm số sát sau - SOSATSAU.PAS Cho số tự nhiên A có N chữ số. Hãy hoán vị các chữ số trong A để thu được số B thoả mãn đồng thời hai điều kiện sau: - B lớn hơn A. - B nhỏ nhất. Dữ liệu vào: Cho trong file SOSATSAU.INP có cấu trúc như sau: - Dòng 1: Ghi số N là số lượng chữ số của A (0a[i-1]. Do đoạn cuối giảm dần, điều này thực hiện bằng cách tìm từ cuối dãy lên đầu gặp chỉ số k đầu tiên thỏa mãn a[k]>a[i-1] (có thể dùng tìm kiếm nhị phân) - Đảo giá trị a[k] và a[i-1] - Lật ngược thứ tự đoạn cuối giảm dần (từ a[i] đến a[k]) trở thành tăng dần + Nếu không tìm thấy tức là toàn dãy đã sắp xếp giảm dần, đây là hoán vị cuối cùng.
Bài 2. MẬT KHẨU. Cu Tí thường xuyên tham gia thi lập trình trên mạng. Vì đạt được thành tích cao nên Tí được gửi tặng một phần mềm diệt virus. Nhà sản xuất phần mềm cung cấp cho Tí một mã số là một dãy gồm các bộ ba chữ số ngăn cách nhau bởi dấu chấm và có chiều dài không quá 255 (kể cả chữ số và dấu chấm). Để cài đặt được phần mềm, Tí phải nhập vào mật khẩu của phần mềm. Mật khẩu là một số nguyên dương M được tạo ra bằng cách tính tổng giá trị các bộ ba chữ số trong dãy mã số, các bộ ba này được đọc từ phải sang trái. - Yêu cầu: Cho biết mã số của phần mềm, hãy tìm mật khẩu của phần mềm đó. - Dữ liệu vào: Cho từ tệp văn bản có tên BL2.INPgồm một dòng chứa xâu ký tự S (độ dài xâu không quá 255 ký tự) là mã số của phần mềm. - Kết quả: Ghi ra tệp văn bản có tên BL2.OUTgồm một số nguyên là mật khẩu tìm được. MK.INP MK.OUT 123.234 257
Bài 6: Biến đổi số BIENDOI.PAS Cho một số nguyên dương M có K chữ số (0 < M; 1 ≤ K ≤ 200). Người ta thực hiện biến đổi số M bằng cách xóa đi trong M các chữ số 0 và sau đó sắp xếp các chữ số còn lại theo thứ tự không giảm của giá trị từng chữ số. Gọi số nguyên dương N là số thu được sau khi thực hiện biến đổi số M. Yêu cầu: Hãy tìm số nguyên dương N. Dữ liệu vào: Nhập vào từ tệp biendoi.inp số M Dữ liệu ra: Ghi ra tệp biendoi.out số N Ví dụ: M=3880247 N=234788
em ko rõ lớp nào làm được bài toán này nên em chỉ chọn đại 1 lớp thôi, bài toán này chỉ thuộc dạng giải phương trình thôi nhưng em thấy khó quá -_-có biến x và tập hợp dãy số nguyên K ( K[1], K[2], K[3], ... , K[n])có tập hợp dãy số nguyên mod (mod[1], mod[2], mod[3], ..., mod[n]) với mỗi phần tử trong tập hợp mod đc tính theo công thức:mod[i] k[i] % x ( % là phép toán chia lấy phần dư, i là chỉ số phần tử tương ứng có trong K và mod).có tập hợp dãy số nguyên int (int[1], int[2], int[3], ..., i...
Đọc tiếp
em ko rõ lớp nào làm được bài toán này nên em chỉ chọn đại 1 lớp thôi, bài toán này chỉ thuộc dạng giải phương trình thôi nhưng em thấy khó quá -_-
có biến x và tập hợp dãy số nguyên K ( K[1], K[2], K[3], ... , K[n])
có tập hợp dãy số nguyên mod (mod[1], mod[2], mod[3], ..., mod[n]) với mỗi phần tử trong tập hợp mod đc tính theo công thức:
mod[i] = k[i] % x ( % là phép toán chia lấy phần dư, i là chỉ số phần tử tương ứng có trong K và mod).
có tập hợp dãy số nguyên int (int[1], int[2], int[3], ..., int[n]) với mỗi phần tử trong tập hợp int đc tính theo công thức:
mod[i] = k[i] / x ( / là phép toán chia lấy phần nguyên, i là chỉ số phần tử tương ứng có trong K và int).
smod là tổng của các phần tử có trong tập hợp mod ( smod = mod[1] + mod[2] + mod[3] + ... + mod[n] )
sint là à tổng của các phần tử có trong tập hợp int (sint = int[1] + int[2] + int[3] + ... + int[n])
T đc tính theo công thức sau : \(T = smod - sint - 12 * n\) (n là số phần tử của K như ở trên).
Ví dụ: có x = 922, tập hợp K có : K[1] = 3572 , K[2] = 3427 , K[3] = 7312 thì ta có:
mod[1] = 806, mod[2] = 661, mod[3] = 858
int[1] = 3, int[2] = 3, int[3] = 7
từ đó có smod = 2325 và sint = 13
K có 3 phần tử nên n = 3, từ đó có T =
T = 2325 - 13 - 12*3 = 2276
Giờ em đã có T và tập hợp K, tức là đã biết T và K[1], K[2], K[3], ..., K[n], lập công thức tính x
Em phải làm thế nào ạ ?
Bài 1: Cho dãy số u1 2; u2 20; Un+1 2Un + Un-1 ( n ≥ 2)a) Viết quy trình ấn phím liên tục tính Un và Sn ( với Sn u1 + u2 +…+ un)b) TÍnh Un; Sn với n 20; n 30Bài 2: Cho dãy số được xác định bởi: u1 1; u2 2;U_{n+2}hept{begin{cases}2U_{n+1}+3U_nleft(n:leright)2U_n+3U_{n+1}left(n:chanright)end{cases}}a) Tính giá trị u10; u15; u21.b) Gọi Sn là tổng của n số hạng đầu tiên của dãy số Un . Tính S10;S15; S20Mong mn giup do
Đọc tiếp
Bài 1: Cho dãy số u1= 2; u2 = 20; Un+1 = 2Un + Un-1 ( n ≥ 2)
a) Viết quy trình ấn phím liên tục tính Un và Sn ( với Sn = u1 + u2 +…+ un)
b) TÍnh Un; Sn với n =20; n = 30
Bài 2: Cho dãy số được xác định bởi: u1 = 1; u2 = 2;\(U_{n+2}=\hept{\begin{cases}2U_{n+1}+3U_n\left(n:le\right)\\2U_n+3U_{n+1}\left(n:chan\right)\end{cases}}\)
a) Tính giá trị u10; u15; u21.
b) Gọi Sn là tổng của n số hạng đầu tiên của dãy số Un . Tính S10;S15; S20
Mong mn giup do
1. Chứng minh rằng \(\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}==2\cos\frac{\pi}{2^{n+1}}\)( n dấu căn)
2.Cho dãy số un = 3n – 1 2n + 1
a) Xác định 5 số hạng đầu tiên
b) số 17 15 là số hạng thứ mấy của dãy số
c) số 32 7 là số hạng thứ mấy của dãy số
cho dãy số : a1=3 ; a2=4 ; a3=6 ; ... ; an+1=a1+n
a ) số thứ 2007 của số trên là số nào ?
b) tính tổng 100 số hạng đầu tiên của dãy số trên ?
Cho hình bình hành ABCD với AB1, ADx (x 0) và
∠
BAD
60
°
Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần
S
1
của hình tạo thành khi quay quanh cạnh AD
Đọc tiếp
Cho hình bình hành ABCD với AB=1, AD=x (x > 0) và ∠ BAD = 60 °
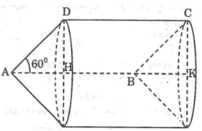
Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S 1 của hình tạo thành khi quay quanh cạnh AD
Cho 2 dãy số : 1,4,7,10
9,16,23,30
Gọi S là tập hợp phần tử giống nhau của cả 2 dãy
Viết công thức tổng quát các phần tử của S
*Bạn nào giải đc cho mình cảm ơn nha*^^^^
Trong buổi họp sơ kết học kì 1 năm 2018-2019 của trường THCS A dự kiến có 120 người dự họp,nhưng khi họp có 160 người tham dự nên phải kê thêm 2 dãy ghế và mỗi dãy phải kê thêm một ghế nữa thì vừa đủ.Tính số dãy ghế dự định lúc đầu,biết rằng số dãy ghế lúc đầu trong phòng nhiều hơn 20 dãy ghế và số ghế trên mỗi dãy ghế là bằng nhau
.. giờ Câu 19: Cho dãy số: 1, 3, 5, 7, 9, …, …, …, Viết tiếp 3 số nữa vào dãy số trên.11, 13, 15Số 20 có nằm trong dãy không? khôngBắt đầuHết giờBắt đầuHết giờ Câu 9: Chu vi hình ... cm16 cmBắt đầuHết giờ ã Cõu 15: S cn in vo du * là: 152 X * 4563Bắt đầuHết giờ 9 và 2Câu 21: Tìm hai số có tích là 18, tổng là 11Bắt đầuHết giờ ãCõu 3: Kt qu ca phộp chia...










