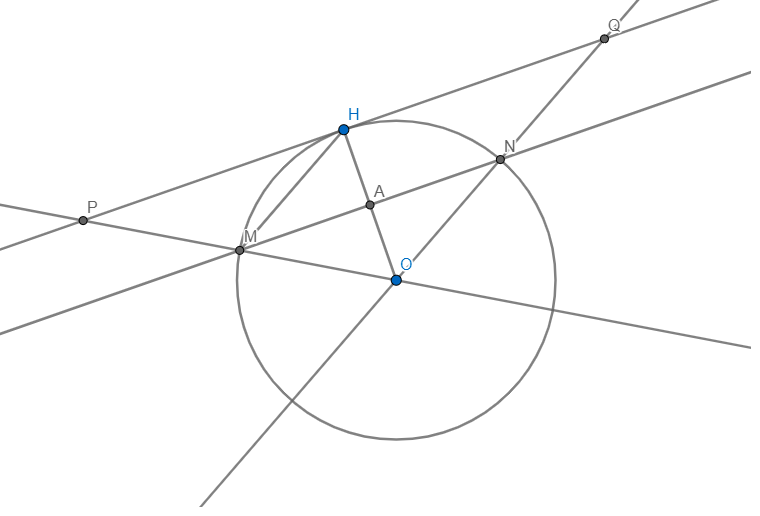
MN cắt OH tại A.
Vì MN là trung trực \(\Rightarrow MN\bot OH\) và A là trung điểm OH
mà \(PQ\bot OH\) \(\Rightarrow PQ\parallel MN\)
Xét \(\Delta OHQ\) có A là trung điểm OH và \(AN\parallel HQ\)
\(\Rightarrow N\) là trung điểm OQ
Tương tự \(\Rightarrow M\) là trung điểm OP
\(\Rightarrow MN\) là đường trung bình tam giác OPQ
\(\Rightarrow PQ=2MN\)
Vì MN là trung trực OH \(\Rightarrow MH=MO=OH\left(=R\right)\Rightarrow\Delta MOH\) đều
\(\Rightarrow MA=sinMHA.MH=sin60.R=\dfrac{\sqrt{3}}{2}R\Rightarrow MN=\sqrt{3}R\)
\(\Rightarrow PQ=2\sqrt{3}R\)