Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B
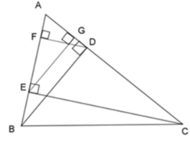
Cho tam giác nhọn ABC : BD và CE là đường cao. Từ D kẻ DF sao cho DF vuông góc AB, từ E kẻ EG sao cho vuông góc AC.
a) CM : AD.AE=AB.AG=AC.AF
b) CM : FG // BC
Cho tam giác nhọn ABC, hai đường cao BD và CE. Qua D kẻ DF vuông góc với AB (F thuộc AB); qua E kẻ EG vuông góc với AC. Chứng minh:
a) A D . A E = A B . A G = A C . AF;
b) FG song song với BC
cho tam giác abc nhọn 2 đuong cao BD;CE .qua D kẻ DF vuông gok vs AB qua E kẻ EG vuông gok vs AC.chm:
a)AD.AE=AB.AG=AC.AF
b)FG//BC
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định không đúng?
A. AD.AE=AB.AG
B. AD.AE = AC.AF
C. AD.AE = AC.FD
D. AE.EG = AB.BD
cho tam giác nhọn ABC.Đường cao BD và CE.Qua D kẻ DF vuông góc với AB tại F.Kẻ EG vuông góc với AC tại G.Chứng minh rằng:
a,AD.AE=AB.AG=AC.AF
b,FG//BC
Cho tam giác ABC các đường cao BD và CE và các đường cao DF ,EG của tam giác ADE
a.Cm AD.AE=AB.AG=AC.AE
b.CM FG//BC
M.n giúp mk với mk cần gấp ( mk cho 5 tích )
B1 cho tam giác abc vuông tại a có đườg cao ah .c/m hệ thức
1 ab^2 = bh.bc và ac^2 = ch.bc
2 ab^2+ac^2=bc^2
3 ah^2=bh.ch
4 ah.bc=ab.ac
Bài 2 cho tam giác abc nhọn .kẻ đường cao bd và ce .vẽ các đường cao df và eg của tam giác ade.c/m
A tam giác abd đồg dạg tam giác aeg
B ad.ae= ab.ag=ac.af
C fg// bc
1.Cho tam giác ABC cân tại A có AB = AC = 5cm, Bc= 6cm. Đường phân giác AD, BE, CF.
a)Tính EF.
b)Tính diện tích tam giác DEF
2. Kẻ đường cao BD và CE của tam giác ABC và các đường cao DF và EG của tam giác ADE.
a) C/m: AD.AE = AB.AG = AC.AF
b)C/m: FG//BC
3.Qua điểm I nằm bên trong tam giác ABC, dựng 3 đường thẳng // với các cạnh của tam giác: DE//BC, MN//CA, PQ//AB (D,M thuộc Ab; N,P thuộc BC; E,Q thuộc AC).CMR: (BD/BA) + (AQ/AC) + (CN/CB) = 1
Bài 12: Cho hình thang ABCD có hai đáy là AB và CD, M là trung điểm của AB, O là giao điểm của AB và CD. OM cắt CD tại N. Chứng minh N là trung điểm CD.
Bài 13: Cho tam giác nhọn ABC, hai đường cao BD và CE. Qua D kẻ DF vuông góc với AB (F∈ AB); qua E kẻ EG vuông góc với AC. Chứng minh:
a) AD.AE=AB.AG=AC.AF
b) FG song song với BC.
