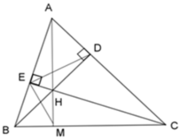
Theo cmt ta có: ΔHBE ~ ΔHCD
⇒ H E H D = H B H C ⇔ H E H B = H D H C
Xét ΔHED và ΔHBC ta có:
H E H B = H D H C (chứng minh trên)
E H D ^ = H A E ^ (hai góc đối đỉnh)
H D E ^ = H A E ^
=> ΔHED ~ ΔHBC (c - g - c)
⇒ H D E ^ = H C B ^ (1)
Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)
=> H là trực tâm của ΔABC
=> AH BC tại M => AMB = 90 ∘
Xét ΔAMB và ΔCEB có:
C E B ^ = A M B ^ = 90 ∘
B chung
=> ΔAMB ~ ΔCEB (g - g)
⇒ M A B ^ = E C B ^ hay H A E ^ = H C B ^ (2)
Từ (1) và (2) ta có: H D E ^ = H A E ^ nên A, B, C đúng, D sai.
Đáp án: D










