`\color{blue}\text {#DuyNam}`
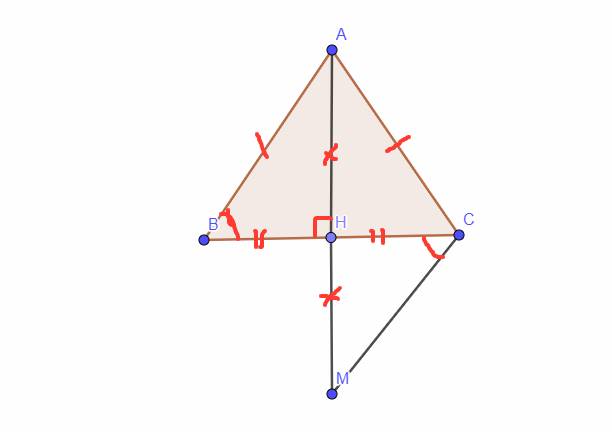
`a,` Xét Tam giác `AHB` và Tam giác `AHC` có:
`AB = AC (g``t)`
`AH` chung
`HB = HC (g``t)`
`=>` Tam giác `AHB =` Tam giác `AHC (c-c-c)`
`b,` Chứng minh `AH \bot BC` cậu nhỉ`?`
Vì Tam giác `AHB =` Tam giác `AHC (a)`
`->` \(\widehat{AHB}=\widehat{AHC}\) `(2` góc tương ứng `)`
Mà `2` góc này nằm ở vị trí kề bù `->`\(\widehat{AHB}+\widehat{AHC}=180^0\)
`->`\(\widehat{AHB}=\widehat{AHC}=\)`180/2=90^0`
`-> AH \bot BC`
`c,` Trên tia đối của `AH` lấy điểm `M` chứ nhỉ`?`
Xét Tam giác `AHB` và Tam giác `CHM` có:
`AH = HM (g``t)`
\(\widehat{AHB}=\widehat{CHM}\) `(2` góc đối đỉnh `)`
`BH=HC (g``t)`
`=>` Tam giác `AHB =` Tam giác `CHM (c-g-c)`
`->`\(\widehat{ABH}=\widehat{MCH}\) `(2` góc tương ứng `)`
Mà `2` góc này nằm ở vị trí sole trong `-> AB`//` CM`