Lấy điểm M( 2+ 2t; 3+ t) nằm trên d;
![]()
Để AM= 5 khi và chỉ khi
(2t+2) 2+ (t+2) 2= 25 hay 5t2+12t- 17= 0
Suy ra t= 1 hoặc t= - 17/5
Với t= 1 thì M( 4;4)
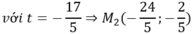
Chọn C.
Lấy điểm M( 2+ 2t; 3+ t) nằm trên d;
![]()
Để AM= 5 khi và chỉ khi
(2t+2) 2+ (t+2) 2= 25 hay 5t2+12t- 17= 0
Suy ra t= 1 hoặc t= - 17/5
Với t= 1 thì M( 4;4)
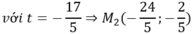
Chọn C.
Đường thẳng d đi qua điểm M(2;-3) và vuông góc với đường thẳng d ' : x = 2 - t y = 3 - 2 t , t ∈ ℝ có phương trình:
A. x + 2y + 4 = 0
B. 2x + 3y + 4 = 0
C. 2x - 3y + 1 = 0
D. x - 2y - 4 = 0
Cho d : x=1+t ; y=2+t . Tìm I trên d sao cho tam giác AIO vuông góc tại I . Biết điểm A(0,-3)
Giao điểm M của đường thẳng d : x = 1 - 2 t y = - 3 + 5 t ( t ∈ ℝ ) và đường thẳng d’: 3x-2y -1= 0 là
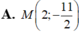
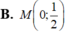
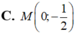
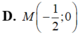
Cho d : x = 2 + 3 t y = 5 - 4 t ( t ∈ ℝ ) . Điểm nào sau đây không thuộc d ?
A. (5; 3)
B. (2; 5)
C.(-1; 9)
D.(8; -3)
Cho đường thẳng d có phương trình tham số x = 2 - 3 t y = - 1 + 2 t ( t ∈ ℝ ) và điểm A(3,5 ; -2). Điểm A thuộc d ứng với giá trị nào của t ?
![]()
![]()
1) Tính khoảng cách từ điểm M đến đường thẳng d, với:
M(3,5); (d): x + y + 1 =0
M(2,3); (d): {x-2t, y = 2 + 3t
M(2,-3); (d): (x - 2)/2 = ( y + 1)/3
2) Viết phưởng trình đường thẳng d song song với đường thẳng △: 2x - y +3 =0 và cách △ một khoảng bằng căn 5
Câu 1: Tìm tập hợp các điểm cách đều 2 đường thẳng:
Delta3 :3x + 4 y + 6 = 0
Delta4 :5x -10 = 0 ( phân giác góc tạo bởi D3 và D4 )
Câu 2: Cho hai đường thẳng:
Delta : 3x + 2y - 1 = 0 và d : 5x - 3y+2=0
1) Tính khoảng cách từ A(5 ;4) đến đường thẳng Delta
2) Viết phương trình các đường phân giác của góc tạo bởi hai đường thẳng trên.
3) Tìm điểm M thuộc Delta sao cho khoảng cách từ M đến d bằng 5.
4) Tìm điểm N thuộc đường thẳng (D1) : x - 2y = 0 bằng hai lần khoảng cách từ N đến d .
Giá trị của tham số m để d:x-2y+3=0 và d ' : x = 3 - m t y = - 2 - 2 t , t ∈ ℝ song song với nhau là:
A. m = 1
B. m = -1
C. m = 4
D. m = -4
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.