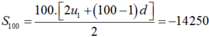
Chọn C.
Đặt a = u1 thì u22 + u32 + u42 = (a + d)2 + (a + 2d)2 + (a + 3d2 = 3a2 – 36a + 126 = 3(a – 6)2 + 18 ≥ 18 với mọi a.
Dấu bằng xảy ra khi a – 6 = 0 hay a = 6.
Suy ra 6 = u1.
Ta có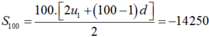 
Cho cấp số cộng ( u n ) có công sai d = - 3 và u 2 2 + u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tính tổng S 100 của 100 số hạng đầu tiên của cấp số cộng đó
A. S 100 = - 14650
B. S 100 = - 14400
C. S 100 = - 14250
D. S 100 = - 15450
Cho cấp số cộng có công sai d=-3 và u22 + u32+ u42 đạt giá trị nhỏ nhất. Tính tổng S100 của 100 số hạng đầu tiên của CSC đó.
Dãy số ( u n ) n = 1 + ∞ là cấp số cộng, công sai d. Tổng S 100 = u 1 + u 2 + . . . + u 100 , u 1 ≠ 0 là
A. S 100 = 2 u 1 + 99 d
B. S 100 = 50 u 100
C. S 100 = 50 u 1 + u 100
D. S 100 = 100 u 1 + u 100
Cho cấp số cộng có công sai d = 1 và u22 – 2u32 – u42 đạt giá trị lớn nhất. Tính tổng S20 của 20 số hạng đầu tiên của cấp số cộng đó.
A.120
B. 125
C.130
D.135
Cho cấp số cộng ( u n ) có công sai d = -4 và u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tìm u 2019 là số hạng thứ 2019 của cấp số cộng đó
A. u 2019 = - 8062
B. u 2019 = - 8060
C. u 2019 = - 8058
D. u 2019 = - 8054
Cho cấp số cộng ( u n ) với số hạng đầu u 1 = - 6 và công sai d = 4. Tính tổng S của 14 số hạng đầu tiên của cấp số cộng đó
A.S = 46
B. S = 308
C. S = 644
D. S = 280
Cho cấp số cộng (un)thoả u2=3 và u10=-15 Tính số hạng đầu u1, công sai d và tổng 20 số hạng đầu tiên của cấp số cộng (un)
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
