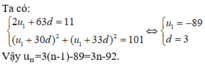Các câu hỏi tương tự
Cho cấp số cộng
(
u
n
)
có số hạng tổng quát là
u
n
3
n
-
2
. Tìm công sai d của cấp số cộng A.
d
3
B. ...
Đọc tiếp
Cho cấp số cộng ( u n ) có số hạng tổng quát là u n = 3 n - 2 . Tìm công sai d của cấp số cộng
A. d = 3
B. d = 2
C. d = - 2
D. d = - 3
Cho cấp số cộng (un) có số hạng đầu là u = 1 và công sai d = 1. Tìm n sao cho tổng n số hạng đầu tiên của cấp số cộng đó bằng 3003
Cho cấp số cộng (
u
n
) có công sai d 0;
u
31
+
u
34
11...
Đọc tiếp
Cho cấp số cộng ( u n ) có công sai d > 0; u 31 + u 34 = 11 u 31 2 + u 34 2 = 101 . Hãy tìm số hạng tổng quát của cấp số cộng đó
A. u n = 3 n - 9
B. u n = 3 n - 2
C. u n = 3 n - 92
D. u n = 3 n - 66
Một cấp số cộng có tổng của n số hạng đầu
S
n
tính theo công thức
S
n
5
n
2
+
3
n
,
(
n
∈
ℕ
*...
Đọc tiếp
Một cấp số cộng có tổng của n số hạng đầu S n tính theo công thức S n = 5 n 2 + 3 n , ( n ∈ ℕ * ) . Tìm số hạng đầu u 1 và công sai d của cấp số cộng đó
A. u 1 = - 8 ; d = 10 .
B. u 1 = - 8 ; d = - 10 .
C. u 1 = 8 ; d = 10 .
D. u 1 = 8 ; d = - 10 .
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Tổng n số hạng đầu tiên của một cấp số cộng là S_n = \frac{3n^2 + 13n}{2}Sn=23n2+13n với n \in \mathbb{N}^*n∈N∗. Số hạng tổng quát của cấp số cộng là
Cho cấp số cộng
u
n
có tổng của n số hạng đầu tiên được tính bởi công thức
S
n
4
n
–
n
^
2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó: A. M -1 B. M 1 C. M 4 D. M 7
Đọc tiếp
Cho cấp số cộng u n có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n – n ^ 2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:
A. M = -1
B. M = 1
C. M = 4
D. M = 7
Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng
u
n
−
3
n
+
1
A.
d
−
2
B.
d
3
C.
d
−
3
D.
d
1
Đọc tiếp
Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng u n = − 3 n + 1
A. d = − 2
B. d = 3
C. d = − 3
D. d = 1
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?