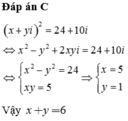Các câu hỏi tương tự
Tìm các số thực x và y, biết:
(3x - 2) + (2y + 1)i = (x + 1) - (y - 5)i
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Tìm các số thực x, y biết 3x - 2 + (y-5)i x + 1 - (2y+1)i
A
.
x
-
3
2
;
y
-
4
3
B
.
x
2
3
;
y
3
4...
Đọc tiếp
Tìm các số thực x, y biết 3x - 2 + (y-5)i = x + 1 - (2y+1)i
A . x = - 3 2 ; y = - 4 3
B . x = 2 3 ; y = 3 4
C . x = - 2 3 ; y = - 3 4
D . x = 3 2 ; y = 4 3
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(x) + f(
π
3
-
x
)
1
2
sin
x
cos
x
(
8
cos
3
x
+
1
)
,
∀
x
∈...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
![]()
![]()
![]()
![]()
Tìm các số thực x và y, biết:
(2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i
Tính tổng tất cả các giá trị của m biết đồ thị hàm số
y
x
3
-
2
mx
2
+
(
m
+
2
)
x
+
4
và đường thẳng y x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng
8
2
với I(1;3) A.3 B. 8 C. 1 D. 5
Đọc tiếp
Tính tổng tất cả các giá trị của m biết đồ thị hàm số y = x 3 - 2 mx 2 + ( m + 2 ) x + 4 và đường thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng 8 2 với I(1;3)
A.3
B. 8
C. 1
D. 5
Cho các Parabol có các đỉnh lần lượt là I1, I2. Gọi A, B là giao điểm của (P1) và Ox. Biết rằng 4 điểm A, B, I1, I2 tạo thành tứ giác lồi có diện tích bằng 10. Tính diện tích S của tam giác IAB với I là đỉnh của Parabol (P): y h(x) f(x) + g(x). (P1): y f(x)
1
4
x
2
-
x
, P(2): y g(x)
a
x
2
-
4
a
x
+
b...
Đọc tiếp
Cho các Parabol có các đỉnh lần lượt là I1, I2. Gọi A, B là giao điểm của (P1) và Ox. Biết rằng 4 điểm A, B, I1, I2 tạo thành tứ giác lồi có diện tích bằng 10. Tính diện tích S của tam giác IAB với I là đỉnh của Parabol (P):
y = h(x) = f(x) + g(x). (P1): y = f(x) = 1 4 x 2 - x , P(2): y = g(x) = a x 2 - 4 a x + b (a>0)
A. S = 6.
B. S = 4.
C. S = 9.
D. S = 7.
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
Tìm các số thực x và y, biết:
(1 - 2x) - i√3 = √5 + (1 - 3y)i