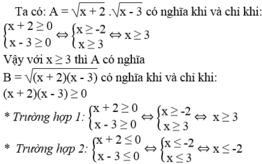
Vậy với x ≥ 3 hoặc x ≤ -2 thì B có nghĩa.
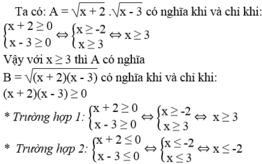
Vậy với x ≥ 3 hoặc x ≤ -2 thì B có nghĩa.
Cho các biểu thức: A = 2 x + 3 x - 3 v à B = 2 x + 3 x - 3
Tìm x để A có nghĩa. Tìm x để B có nghĩa
GIÚP MÌNH VỚI
Cho biểu thức: A= (√x/√x -3 + √x /√x+3): (1-3/√x+3) a) tìm đk để A có nghĩa b)rút gọn A c)Tìm x để A=-1
Cho các biểu thức sau: \(A=\sqrt{\frac{2x+3}{x-3}}\)và \(B=\frac{\sqrt{2x+3}}{\sqrt{x-3}}\)
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
b) Với giá trị nào của x thì A=B?
Tìm x để biểu thức sau có nghĩa:
a)\(\sqrt{\dfrac{x}{3}}\) b) \(\sqrt{-5x}\) c) \(\sqrt{4-x}\) d) \(\sqrt{1+x^2}\)
Cho biểu thức :A=\(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x-2}{x-3\sqrt{x}+2}\)
a) Tìm điều kiện để A có nghĩa và rút gọn A
b) Tìm x để A > 2
c) Tìm số nguyên x sao cho A là số nguyên
cho biểu thức: P=\(\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3x-3}{x-9}\right):\left(\frac{2\sqrt{x}-2}{\sqrt{x}+3}\right)\)
a) tìm điều kiện của x để P có nghĩa
b) rút gọn P
c) tìm các giá trị nguyên của x để P có giá trị nguyên
1. Tính x để căn thức sau có nghĩa:
\(\sqrt{\frac{-2x}{x^2-\text{3}x+9}}\)
2. Tìm các giá trị nguyên của x để các biểu thức sau có nghĩa:
a/A=\(\frac{\sqrt{x}+\text{3}}{\sqrt{x}-2}\)
b/B=\(\frac{2\sqrt{x}-1}{\sqrt{x}+\text{3}}\)
3. Cho biểu thức P= (\(\frac{\sqrt{x}}{\sqrt{x}-1}\)-\(\frac{1}{x-x\sqrt{x}}\): (\(\frac{1}{\sqrt{x}+1}\)+\(\frac{2}{x-1}\))
a/ Tìm điều kiện x để P xđ: Rút gọn
b/ Tìm các giá trị của P để P <0
c/ Tính giá trị của P khi x=4-2\(\sqrt{\text{3}}\)
Câu 3: Cho biểu thức A=\(\dfrac{\sqrt{x}}{\sqrt{x}-1}\) + \(\dfrac{3}{\sqrt{x}+1}\) + \(\dfrac{6\sqrt{x}-4}{1-x}\)
a. Tìm điều kiện của x để A có nghĩa rồi rút gọn A. Tính giá trị của A khi x = 6-2\(\sqrt{5}\)
b. Tìm giá trị của x để A < \(\dfrac{1}{2}\)
c. Tìm giá trị nhỏ nhất của biểu thức A
Cho biểu thức
P= căn x/ căn x-3 -2/căn x+3 + 5 căn x+3/x-9
A) tìm điều kiện để p có nghĩa và rút gọn p
B) tìm x để p = 2