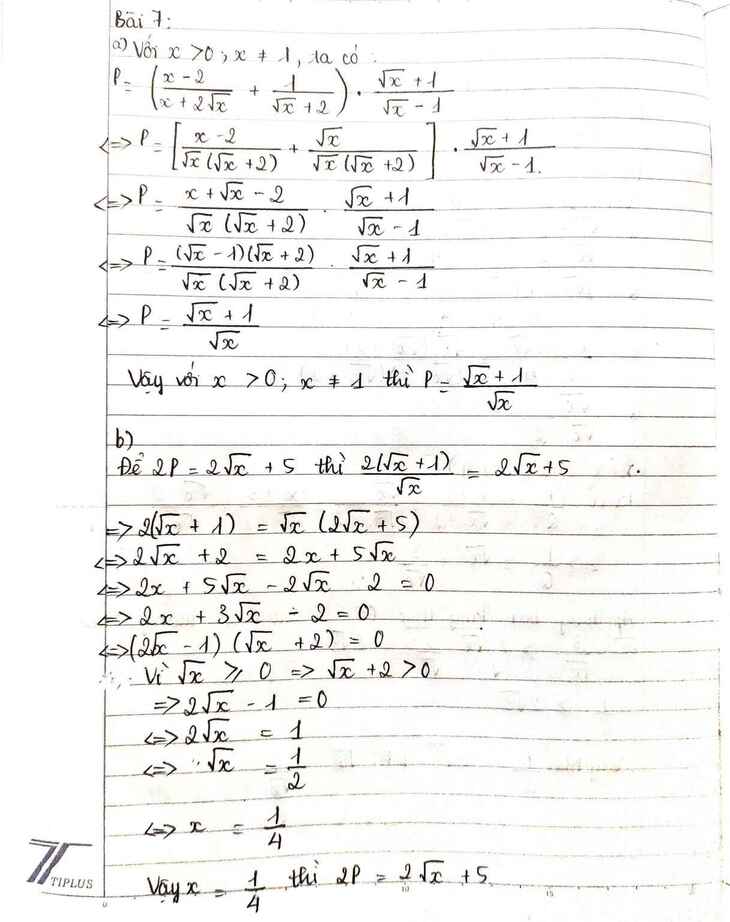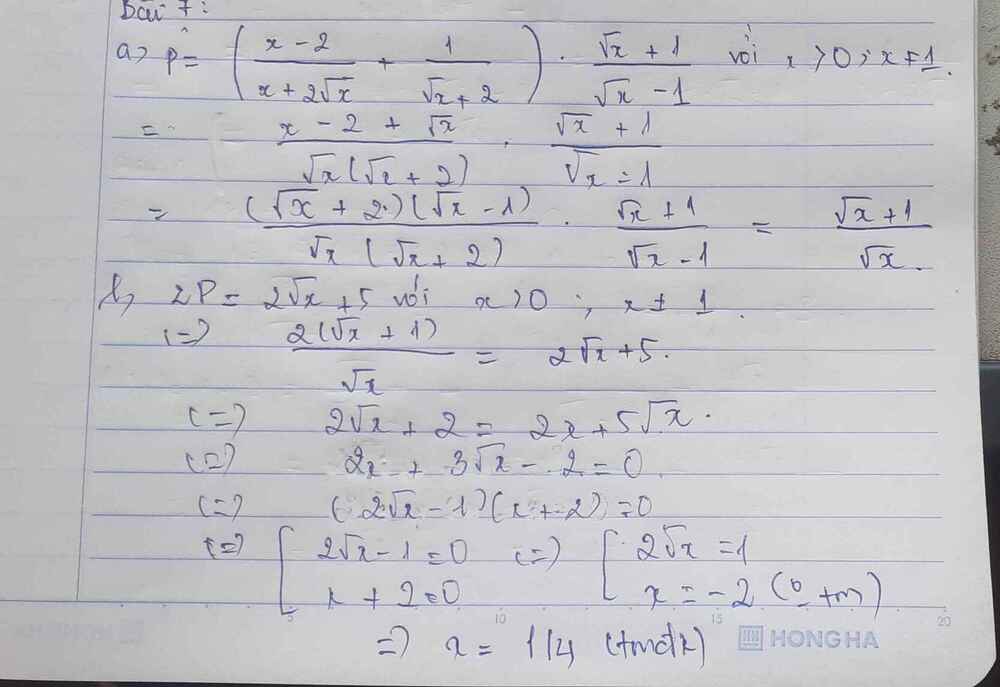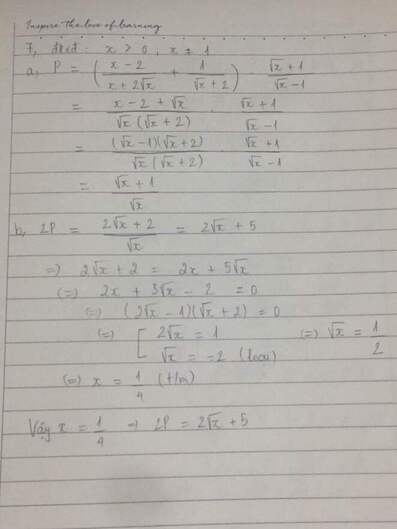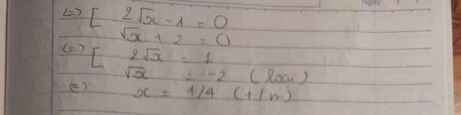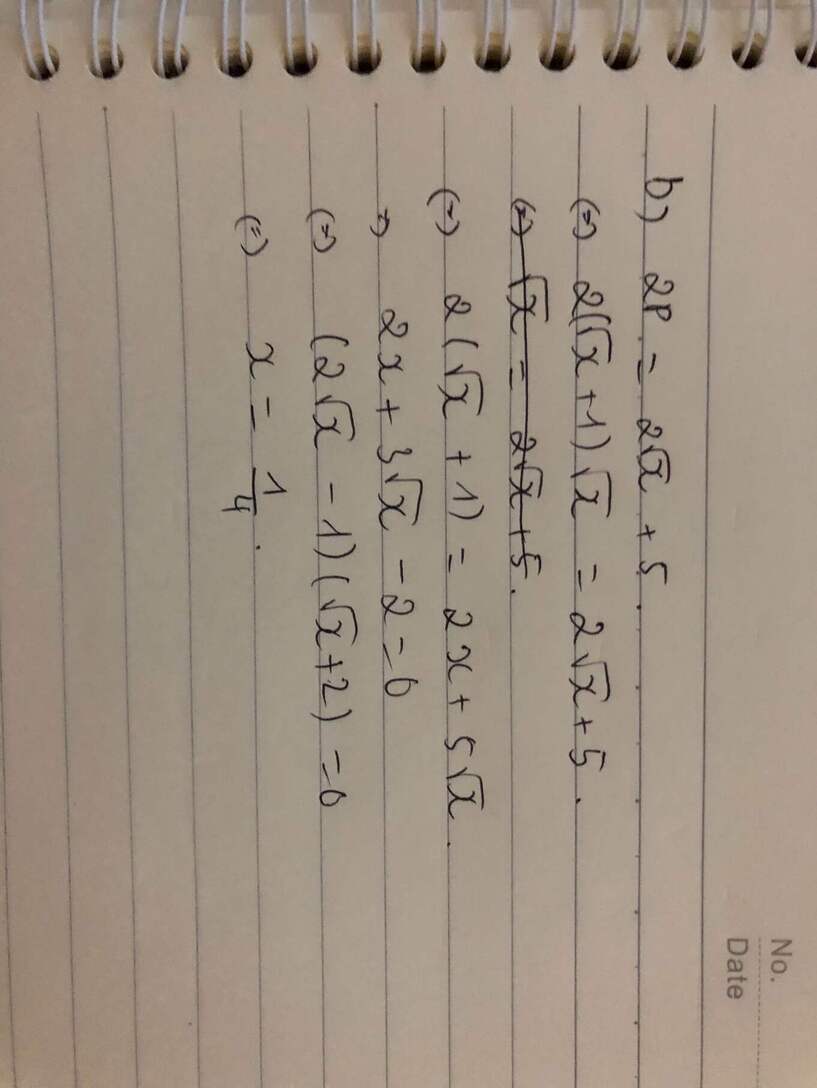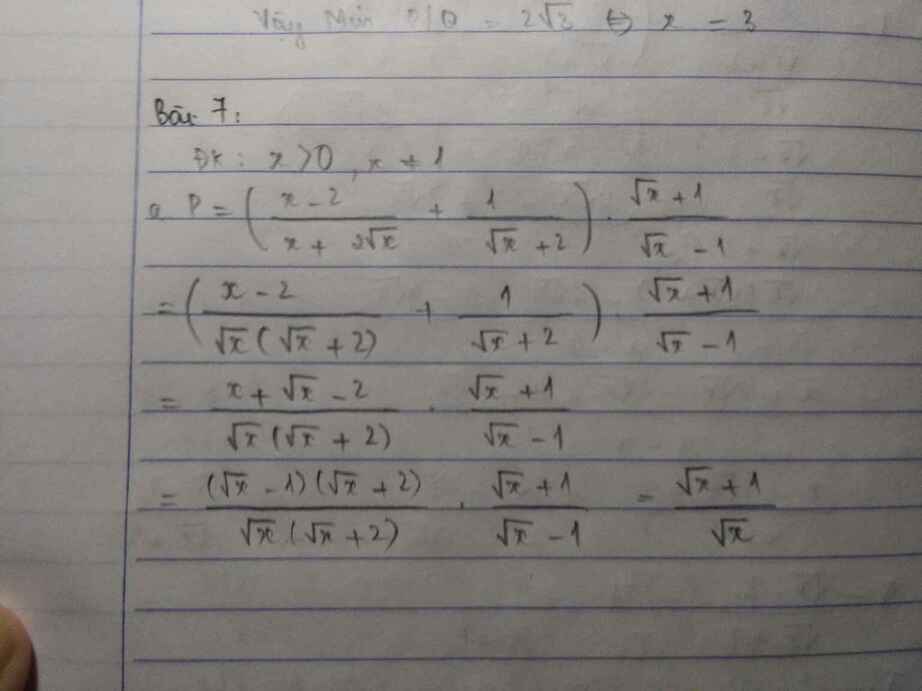Question

Cho biểu thức \(P=\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\) với \(x>0,x\ne1\)

a) Chứng minh \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b) Tìm $x$ để \(2P=2\sqrt{x}+5\).

Answer 1

a) Với \(x>0;x\ne1\), ta có:

\(P=\left(\frac{x-2}{x+2\sqrt{x}}+\frac{1}{\sqrt{x}+2}\right).\frac{\sqrt{x}+1}{\sqrt{x}-1}\)

\(P=\left[\frac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\frac{1}{\sqrt{x}+2}\right].\frac{\sqrt{x}+1}{\sqrt{x}-1}\)

\(P=\left[\frac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right].\frac{\sqrt{x}+1}{\sqrt{x}-1}\)

\(P=\frac{x+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{x}-1}{\sqrt{x}}.\frac{\sqrt{x}+1}{\sqrt{x}-1}\)

\(P=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\frac{\sqrt{x}+1}{\sqrt{x}}\)

Vậy với \(x>0,x\ne1\)thì \(P=\frac{\sqrt{x}+1}{\sqrt{x}}\)

Answer 2

\(P=\frac{\sqrt{x}+1}{\sqrt{x}}\)

\(\Rightarrow2P=\frac{2\sqrt{x}+2}{\sqrt{x}}\)

\(2P=2\sqrt{x}+5\Leftrightarrow\frac{2\sqrt{x}+2}{\sqrt{x}}=2\sqrt{x}+5\left(ĐKXĐ:x\ne0\right)\left(1\right)\)

Mà theo đề bài : \(x>0\)nên phương trình luôn được xác định.

\(\left(1\right)\Leftrightarrow\frac{2\sqrt{x}+2}{\sqrt{x}}=\frac{\sqrt{x}\left(2\sqrt{x}+5\right)}{\sqrt{x}}\)

\(\Rightarrow2\sqrt{x}+2=\sqrt{x}\left(2\sqrt{x}+5\right)\)

\(\Leftrightarrow2\sqrt{x}+2=2x+5\sqrt{x}\)

\(\Leftrightarrow2\sqrt{x}+2-2x-5\sqrt{x}\)

\(\Leftrightarrow-2x-3\sqrt{x}+2=0\Leftrightarrow2x+3\sqrt{x}-2=0\)

\(\Leftrightarrow\left(2\sqrt{x}-1\right)\left(\sqrt{x}+2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}2\sqrt{x}-1=0\\\sqrt{x}+2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2\sqrt{x}=1\\\sqrt{x}=-2\left(vn\right)\end{cases}}\Leftrightarrow2\sqrt{x}=1\)

\(\Leftrightarrow\sqrt{x}=\frac{1}{2}\Leftrightarrow x=\frac{1}{4}\left(TMĐK:x>0;x\ne1\right)\)

Vậy \(2P=2\sqrt{x}+5\Leftrightarrow x=\frac{1}{4}\)

Answer 3

 

b)  2P=2√x+5⇔2(√x+1)√x =2√x+5

⇔2(√x+1)=2x+5√x⇒2x+3√x−2=0

⇔(2√x−1)(√x+2)=0

14.

Answer 4

a,\(P= (\dfrac{x-2}{\sqrt{x}({\sqrt{x}-2})} + \dfrac{1}{\sqrt{x}+2}) . \dfrac{\sqrt{x}+1}{\sqrt{x}-1} = \dfrac{x-2+\sqrt{x}}{\sqrt{x}({\sqrt{x}+2})}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1} = \dfrac{x+\sqrt{x}-2}{\sqrt{x}(\sqrt{x}+2)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1} = \dfrac{\sqrt{x}+1}{\sqrt{x}}\)b,  \(x = \dfrac{1}{2} ; x= -2\)

Answer 5

x=\(\dfrac{1}{4}\)

Answer 6

Answer 7

a,P=\(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\) . \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\) =\(\left(\dfrac{x+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\) =\(\left(\dfrac{\left(\sqrt{x-1}\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\left(đfcm\right)\)                                             b, Để 2P=2\(\sqrt{x}\) +5 khi x=\(\dfrac{1}{4}\)

Answer 8

a/ ĐKXD x>0,x
​≠1

  P= \(\dfrac{x-2+\sqrt{x}}{\sqrt{x}.\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)=\(\dfrac{\sqrt{x}-1}{\sqrt{x}}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

 Vậy P= \(\dfrac{\sqrt{x}+1}{\sqrt{x}}\) với x>0,x
​≠1

 b/  Ta có 2P= \(2\sqrt{x}+5\) ⇒ 2.\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)=\(2\sqrt{x}+5\)⇒ \(2\sqrt{x}+2=2x+5\sqrt{x}=>2x+3\sqrt{x}-2=0\)

                                    ⇔\(\left(2\sqrt{x}-1\right).\left(\sqrt{x}+2\right)=0\)⇒ \(x=\dfrac{1}{4}\left(TMDK\right)\)

 Vậy \(x=\dfrac{1}{4}\left(TMDK\right)\) thì 2P= \(2\sqrt{x}+5\) 

Answer 9

b) x=\(\dfrac{1}{4}\)

Answer 10

a, P = \(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)

    P = \(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b, Ta có 

2P = \(2\sqrt{x}+5\)

\(\Rightarrow x=4\)

Answer 11

 a)    Với x >0 ; x ≠1, ta có

P =\([\dfrac{x-2}{\sqrt{x}(\sqrt{x}+2)}+\dfrac{\sqrt{x}}{\sqrt{x}\times(\sqrt{x}+2)}]\times\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
P =\(\dfrac{x+\sqrt{x}-2}{\sqrt{x}(\sqrt{x}+2)}\times\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

=\(\dfrac{(\sqrt{x}-1)(\sqrt{x}+2)(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+2)(\sqrt{x}-1)}\)

=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

Vậy với x>0 , x≠1, P =\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b)    Để 2P = \(2\sqrt{x}+5\)

⇔\(\dfrac{2\times(\sqrt{x}+1)}{\sqrt{x}}=2\sqrt{x}+5\Leftrightarrow2\sqrt{x}+2=2x+5\sqrt{x}\)

⇔\(2x+3\sqrt{x}-2=0\Leftrightarrow(\sqrt{x}+2)(2\sqrt{x}-1)=0\)

Do \(\sqrt{x}+2>0\forall x\ne1\)⇔\(2\sqrt{x}-1=0\)

⇔\(\sqrt{x}=\dfrac{1}{2}\)

⇔x=\(\dfrac{1}{4}\)( thỏa mãn x>0, x≠1)

Vậy với x= \(\dfrac{1}{4}\) thì 2P =\(2\sqrt{x}+5\)

Answer 12

Answer 13

a) P=\(\dfrac{x+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)}\). \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

P= \(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b) x=\(\dfrac{1}{4}\)

Answer 14

 

Answer 15

 

 

Answer 16

Answer 17

 

Answer 18

 

Answer 19

a,P=\(\dfrac{x+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)}\). \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

P=\(\dfrac{\sqrt{x}-1}{\sqrt{x}}\).\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

P=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b, 2P=\(\dfrac{2\sqrt{x}+2}{\sqrt{x}}=2\sqrt{x}+5\)

=\(2\sqrt{x}+2-2x-5\sqrt{x}\)

=\(\left(2\sqrt{x}-1\right)\left(\sqrt{x}+2\right)=0\)

\(< =>x=\dfrac{1}{4}\)

Answer 20

 

 

Answer 21

 

Answer 22

a) P=\(\dfrac{x-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b) \(2P=2\sqrt{x}+5\Leftrightarrow\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}}=2\sqrt{x}+5\)

\(\Leftrightarrow2\left(\sqrt{x}+1\right)=2x+5\sqrt{x}\Rightarrow2x+3\sqrt{x}-2=0\)

\(\Leftrightarrow\left(2\sqrt{x}-1\right)\left(\sqrt{x}+2\right)=0\)

Đáp số: x= \dfrac 14x=\(\dfrac{1}{4}\)

Answer 23

a) P=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

b) x=\(\dfrac{1}{4}\)

Answer 24

 

Answer 25

Answer 26

 

 

Answer 27

 

Answer 28

 

Answer 29

a, ĐK: $x>0;x\ne 1$

$P=\backslash (\backslash left(\backslash dfrac\{x-2\}\{\backslash sqrt\{x\}\backslash left(\backslash sqrt\{x\}+2\backslash right)\}+\backslash dfrac\{\backslash sqrt\{x\}\}\{\backslash sqrt\{x\}\backslash left(\backslash sqrt\{x\}+2\backslash right)\}\backslash right)\backslash ).\; \backslash (\backslash dfrac\{\backslash sqrt\{x\}+1\}\{\backslash sqrt\{x\}-1\}\backslash )$

$P\; =$\(\dfrac{x+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)}\).\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)(ĐPCM)

b, x=\(\dfrac{1}{4}\)thì 2P= 2\(\sqrt{x}\)+5

Answer 30