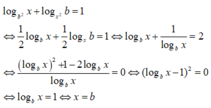Các câu hỏi tương tự
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Tìm x, biết 25 x - 2. 10 x + 4 x = 0
A. x = 1 B. x = -1
C. x = 2 D. x = 0
Trong không gian Oxyz cho A(-1;-1;0), B(0;1;0), M(a;b;c) với (b0) thuộc mặt phẳng (P): x+y+z+20 sao cho
A
M
2
và mặt phẳng (ABM) vuông góc với mặt phẳng (P) Khi đó
T
2
a
-
4
b
2
+
c
bằng A. -8 B. 7 C. 28 D. -17
Đọc tiếp
Trong không gian Oxyz cho A(-1;-1;0), B(0;1;0), M(a;b;c) với (b<0) thuộc mặt phẳng (P): x+y+z+2=0 sao cho A M = 2 và mặt phẳng (ABM) vuông góc với mặt phẳng (P) Khi đó T = 2 a - 4 b 2 + c bằng
A. -8
B. 7
C. 28
D. -17
Tìm x, biết 25 x - 2 . 10 x + 4 x = 0
A. x = 1 B. x = -1
C. x = 2 D. x = 0
Tìm x, biết: 2 x + 3 x = 5 x
A. x = 0 B. x = 1
C. x = -1 D. x = 2
Tìm x, biết: 2 x + 3 x = 5 x .
A. x = 0 B. x = 1
C. x = -1 D. x = 2
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;-3;2), B (3;5;-2). Phương trình mặt phẳng trung trực của AB có dạng x + ay + bz + c 0. Khi đó a + b + c bằng
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A (1;-3;2), B (3;5;-2). Phương trình mặt phẳng trung
trực của AB có dạng x + ay + bz + c =0.
Khi đó a + b + c bằng
![]()
![]()
![]()
![]()
Trong hệ trục tọa độ Oxyz cho 2 điểm A(0; -2; -1) và B(1; -2; 2), mặt phẳng (P): x +2y + 2z 0, AB
∩
(P) N. Khi đó
A
B
B
N
bằng
Đọc tiếp
Trong hệ trục tọa độ Oxyz cho 2 điểm
A(0; -2; -1) và B(1; -2; 2), mặt phẳng
(P): x +2y + 2z = 0, AB ∩ (P) = N.
Khi đó A B B N bằng
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c khác 0 Biết rằng mặt phẳng (ABC) đi qua điểm
M
2
3
;
4
3
;
4
3
và tiếp xúc với mặ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c khác 0 Biết rằng mặt phẳng (ABC) đi qua điểm M 2 3 ; 4 3 ; 4 3 và tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 1 Thể tích khối tứ diện OABC bằng
A. 4
B. 6
C. 9
D. 12